题目内容
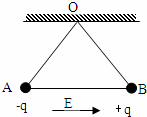
有三根长度皆为L=2.00 m的不可伸长的绝缘轻线,其中两根的一端固定在天花板上的O点,另一端分别拴有质量皆为m=1.00×10-2 kg的带电小球A和B,它们的电量分别为+q和-q,q=1.00×10-7 C.A、B之间用第三根线连接起来.空间中存在大小为E=1.00×106 N/C的匀强电场,场强方向沿水平向右,平衡时A、B球的位置如图所示.现将O、B之间的线烧断,由于有空气阻力,A、B球最后会达到新的平衡位置.(忽略电荷间相互作用力)
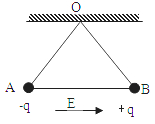
(1)在细线OB烧断前,AB间细绳中的张力大小.
(2)当细绳OB烧断后并重新达到平衡后细绳AB中张力大小?
(3)在重新达到平衡的过程中系统克服空气阻力做了多少的功?
【答案】
(1)0.043 N(2)0.14 N(3)0.1364 J
【解析】
试题分析:(1)在细线OB烧断前,受力分析如图所示:
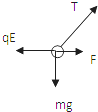
竖直方向上有:Tsin60°=mg 1 分
T=0.115 N 1 分
水平方向上:F=qE-Tcos60°=0.043 N 2 分
(2)平衡后的状态如图所示
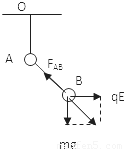
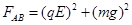 =0.14
N
3 分
=0.14
N
3 分
(3)AB线与水平方向夹角θ,则tanθ==1
所以 θ=45° 1 分
所以重力做功:WG=mgL(1-sin60°+1+sin45°-sin60°)=0.195 J 2 分
电场力做功:WE=qEL(-sin30°+sin45°-sin30°)=-0.0586 J 2 分
所以克服阻力的功:Wf=WG+WE=0.1364 J 1 分
考点:本题考查电场力和电场力做功。

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
 (2002?天津)有三根长度皆为l=1.00m的不可伸长的绝缘轻线,其中两根的一端固定在天花板上的 O点,另一端分别挂有质量皆为m=1.00×10-2 kg的带电小球A和B,它们的电量分别为一q和+q,q=1.00×10-7C.A、B之间用第三根线连接起来.空间中存在大小为E=1.00×106N/C的匀强电场,场强方向沿水平向右,平衡时 A、B球的位置如图所示.现将O、B之间的线烧断,由于有空气阻力,A、B球最后会达到新的平衡位置.求最后两球的机械能与电势能的总和与烧断前相比改变了多少.(不计两带电小球间相互作用的静电力)
(2002?天津)有三根长度皆为l=1.00m的不可伸长的绝缘轻线,其中两根的一端固定在天花板上的 O点,另一端分别挂有质量皆为m=1.00×10-2 kg的带电小球A和B,它们的电量分别为一q和+q,q=1.00×10-7C.A、B之间用第三根线连接起来.空间中存在大小为E=1.00×106N/C的匀强电场,场强方向沿水平向右,平衡时 A、B球的位置如图所示.现将O、B之间的线烧断,由于有空气阻力,A、B球最后会达到新的平衡位置.求最后两球的机械能与电势能的总和与烧断前相比改变了多少.(不计两带电小球间相互作用的静电力)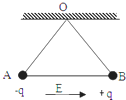 有三根长度皆为L=2.00m的不可伸长的绝缘轻线,其中两根的一端固定在天花板上的O点,另一端分别拴有质量皆为m=1.00×10-2Kg的带电小球A和B,它们的电量分别为+q和-q,q=1.00×10-7C.A、B之间用第三根线连接起来.空间中存在大小为E=1.00×106N/C的匀强电场,场强方向沿水平向右,平衡时A、B球的位置如图所示.现将O、B之间的线烧断,由于有空气阻力,A、B球最后会达到新的平衡位置.(忽略电荷间相互作用力)
有三根长度皆为L=2.00m的不可伸长的绝缘轻线,其中两根的一端固定在天花板上的O点,另一端分别拴有质量皆为m=1.00×10-2Kg的带电小球A和B,它们的电量分别为+q和-q,q=1.00×10-7C.A、B之间用第三根线连接起来.空间中存在大小为E=1.00×106N/C的匀强电场,场强方向沿水平向右,平衡时A、B球的位置如图所示.现将O、B之间的线烧断,由于有空气阻力,A、B球最后会达到新的平衡位置.(忽略电荷间相互作用力)