题目内容
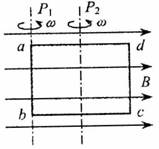
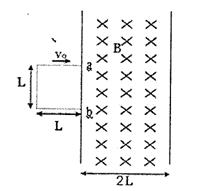
磁悬浮列车是一种高速运载工具,它由两个系统组成。一是悬浮系统,利用磁力使车体在轨道上悬浮起来从而减小阻力。另一是驱动系统,即利用磁场与固定在车体下部的感应金属线圈相互作用,使车体获得牵引力,图22就是这种磁悬浮列车电磁驱动装置的原理示意图。即在水平面上有两根很长的平行轨道PQ和MN,轨道间有垂直轨道平面的匀强磁场B1和B2,且B1和B2的方向相反,大小相等,即B1=B2=B。列车底部固定着绕有N匝闭合的矩形金属线圈abcd(列车的车厢在图中未画出),车厢与线圈绝缘。两轨道间距及线圈垂直轨道的ab边长均为L,两磁场的宽度均与线圈的ad边长相同。当两磁场Bl和B2同时沿轨道方向向右运动时,线圈会受到向右的磁场力,带动列车沿导轨运动。已知列车车厢及线圈的总质量为M,整个线圈的总电阻为R。
(1)假设用两磁场同时水平向右以速度v0作匀速运动来起动列车,为使列车能随磁场运动,列车所受的阻力大小应满足的条件;
(2)设列车所受阻力大小恒为f,假如使列车水平向右以速度v做匀速运动,求维持列车运动外界在单位时间内需提供的总能量;
(3)设列车所受阻力大小恒为f,假如用两磁场由静止开始向右做匀加速运动来起动列车,当两磁场运动的时间为t1时,列车正在向右做匀加速直线运动,此时列车的速度为v1,求两磁场开始运动到列车开始运动所需要的时间t0。
(1)假设用两磁场同时水平向右以速度v0作匀速运动来起动列车,为使列车能随磁场运动,列车所受的阻力大小应满足的条件;
(2)设列车所受阻力大小恒为f,假如使列车水平向右以速度v做匀速运动,求维持列车运动外界在单位时间内需提供的总能量;
(3)设列车所受阻力大小恒为f,假如用两磁场由静止开始向右做匀加速运动来起动列车,当两磁场运动的时间为t1时,列车正在向右做匀加速直线运动,此时列车的速度为v1,求两磁场开始运动到列车开始运动所需要的时间t0。

(1)列车静止时,电流最大,列车受到的电磁驱动力最大设为Fm,此时,线框中产生的感应电动势 E1=2NBLv0
线框中的电流 I1=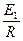
整个线框受到的安培力 Fm=2NBI1L
列车所受阻力大小为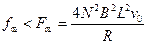 (4分)
(4分)
(2)当列车以速度v匀速运动时,两磁场水平向右运动的速度为v′,金属框中感应电动势

金属框中感应电流
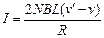
又因为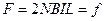
求得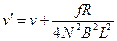 (2分)
(2分)
当列车匀速运动时,金属框中的热功率为 P1 = I2R
克服阻力的功率为 P2 = fv
所以可求得外界在单位时间内需提供的总能量为
E= I2R +fv= (2分)
(2分)
(3)根据题意分析可得,为实现列车最终沿水平方向做匀加速直线运动,其加速度必须与两磁场由静止开始做匀加速直线运动的加速度相同,设加速度为a,则t1时刻金属线圈中的电动势
金属框中感应电流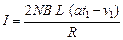
又因为安培力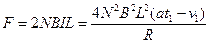
所以对列车,由牛顿第二定律得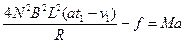
解得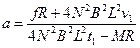
 (2分)
(2分)
设从磁场运动到列车起动需要时间为t0,则t0时刻金属线圈中的电动势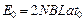
金属框中感应电流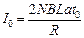
又因为安培力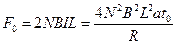
所以对列车,由牛顿第二定律得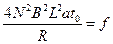
解得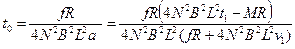
 (2分)
(2分)
线框中的电流 I1=
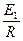
整个线框受到的安培力 Fm=2NBI1L
列车所受阻力大小为
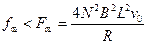 (4分)
(4分)(2)当列车以速度v匀速运动时,两磁场水平向右运动的速度为v′,金属框中感应电动势

金属框中感应电流
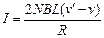
又因为
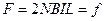
求得
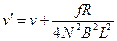 (2分)
(2分)当列车匀速运动时,金属框中的热功率为 P1 = I2R
克服阻力的功率为 P2 = fv
所以可求得外界在单位时间内需提供的总能量为
E= I2R +fv=
 (2分)
(2分)(3)根据题意分析可得,为实现列车最终沿水平方向做匀加速直线运动,其加速度必须与两磁场由静止开始做匀加速直线运动的加速度相同,设加速度为a,则t1时刻金属线圈中的电动势

金属框中感应电流
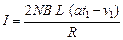
又因为安培力
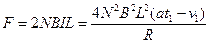
所以对列车,由牛顿第二定律得
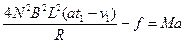
解得
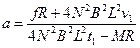
 (2分)
(2分)设从磁场运动到列车起动需要时间为t0,则t0时刻金属线圈中的电动势
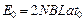
金属框中感应电流
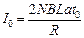
又因为安培力
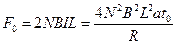
所以对列车,由牛顿第二定律得
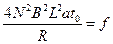
解得
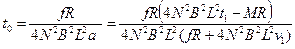
 (2分)
(2分)略

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
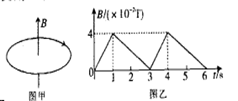
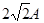
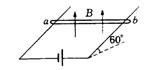


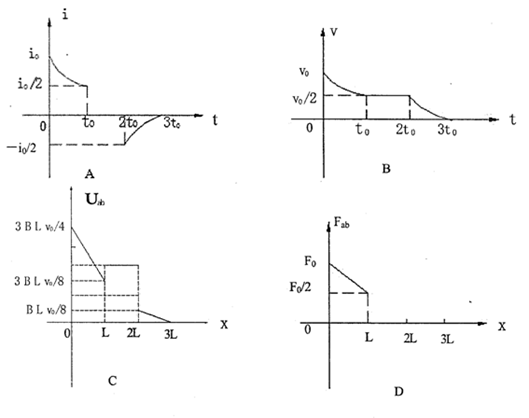
 (特斯拉)。灯丝发出的电子经过加速电压为U=125V的电场加速后,垂直磁场方向进入匀强磁场区域,通过标尺测得圆形径迹的直径为D = 80.0mm,请估算电子的比荷
(特斯拉)。灯丝发出的电子经过加速电压为U=125V的电场加速后,垂直磁场方向进入匀强磁场区域,通过标尺测得圆形径迹的直径为D = 80.0mm,请估算电子的比荷 。(答案保留2位有效数字)
。(答案保留2位有效数字)