题目内容
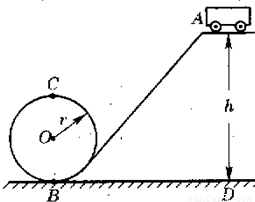
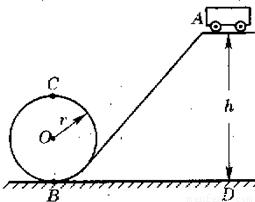
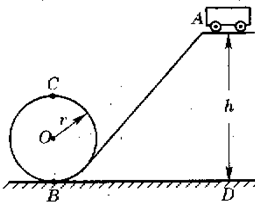 过山车是一种惊险的游乐工具,其运动轨道可视为如图所示的物理模型.已知轨道最高点A离地面高为20m,圆环轨道半径为5m,过山车质量为50kg,g=10m/s2,求:
过山车是一种惊险的游乐工具,其运动轨道可视为如图所示的物理模型.已知轨道最高点A离地面高为20m,圆环轨道半径为5m,过山车质量为50kg,g=10m/s2,求:(1)若不计一切阻力,该车从A点静止释放后,经过最低点B时的速度为多大?
(2)若不计一切阻力,当过山车经过圆形轨道最高点C时,轨道对车的作用力为多大?
(3)若考虑阻力的影响,当过山车经过C点时对轨道恰好无压力,则在过山车从A点运动至C点的过程中,克服阻力做的功为多大?
分析:(1)在运动的过程中只有车的重力做功,根据动能定理可以求得车到达最低点的速度的大小;
(2)由机械能守恒可以求得车在C点的速度的大小,再根据向心力的公式可以求得轨道对车的作用力的大小;
(3)当过山车经过C点时对轨道恰好无压力,说明此时恰好只有车的重力作为向心力,从而可以求得车在C点的速度的大小,再由动能定理可以求得阻力做的功.
(2)由机械能守恒可以求得车在C点的速度的大小,再根据向心力的公式可以求得轨道对车的作用力的大小;
(3)当过山车经过C点时对轨道恰好无压力,说明此时恰好只有车的重力作为向心力,从而可以求得车在C点的速度的大小,再由动能定理可以求得阻力做的功.
解答:解:(1)由mgh=
mv2
可知 V=
=20m/s,
(2)A到C的过程中,由机械能守恒可知:mg(h-2r)=
m
,
解得 Vc=
=10
m/s,
在C点时由:F+mg=m
解答 F=1500N.
(3)A到C的过程中,由动能定理可知:mg(h-2r)-W=
m
(1)
又因为山车经过C点时对轨道恰好无压力,所以:mg=m
(2)
由(1)(2)可知:W=mg(h-2r)-
m
=mg(h-2r)-
mgr
=3750J,
答:(1)经过最低点B时的速度为20m/s.
(2)当过山车经过圆形轨道最高点C时,轨道对车的作用力为1500N.
(3)过山车从A点运动至C点的过程中,克服阻力做的功为3750J.
| 1 |
| 2 |
可知 V=
| 2gh |
(2)A到C的过程中,由机械能守恒可知:mg(h-2r)=
| 1 |
| 2 |
| V | 2 c |
解得 Vc=
| 2g(h-2r) |
| 2 |
在C点时由:F+mg=m
| ||
| r |
解答 F=1500N.
(3)A到C的过程中,由动能定理可知:mg(h-2r)-W=
| 1 |
| 2 |
| V | 2 c |
又因为山车经过C点时对轨道恰好无压力,所以:mg=m
| ||
| r |
由(1)(2)可知:W=mg(h-2r)-
| 1 |
| 2 |
| V | 2 c |
=mg(h-2r)-
| 1 |
| 2 |
=3750J,
答:(1)经过最低点B时的速度为20m/s.
(2)当过山车经过圆形轨道最高点C时,轨道对车的作用力为1500N.
(3)过山车从A点运动至C点的过程中,克服阻力做的功为3750J.
点评:解答本题的关键在于理解“过山车经过C点时对轨道恰好无压力”这句话的含义,本题属于圆周运动中绳的模型,在最高点时应该是重力恰好做为圆周运动的向心力,对于圆周运动中的两种模型一定要牢牢的掌握住.

练习册系列答案
相关题目
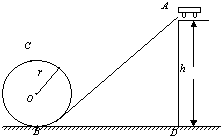 过山车是一种惊险的游乐工具,其运动轨道可视为如图14所示物理模型.已知轨道最高点A离地面高为12.8m,圆环轨道半径为5m,过山车质量为150kg,g取10m/s2.
过山车是一种惊险的游乐工具,其运动轨道可视为如图14所示物理模型.已知轨道最高点A离地面高为12.8m,圆环轨道半径为5m,过山车质量为150kg,g取10m/s2. 过山车是一种惊险的游乐工具,其运动轨道可视为如图所示的物理模型.已知轨道最高点A离地面高为h=12.8m,圆环轨道半径为R=5m,过山车质量为m=150kg,重力加速度g取10m/s2,求:
过山车是一种惊险的游乐工具,其运动轨道可视为如图所示的物理模型.已知轨道最高点A离地面高为h=12.8m,圆环轨道半径为R=5m,过山车质量为m=150kg,重力加速度g取10m/s2,求: