题目内容
3. 如甲图所示,劲度系数为k的轻质弹簧的下端固定在水平面上,上端叠放两个物体A、B,B的质量为m.初始时物体处于静止状态.现用竖直向上的拉力作用在物体A上,使物体A开始向上做匀加速直线运动,测得两个物体的速度υ-t图象如图乙所示,图中υ1、υ2、t1、t2已知,重力加速度为g,求:t1~t2时间内,弹簧弹性势能减少了多少?
如甲图所示,劲度系数为k的轻质弹簧的下端固定在水平面上,上端叠放两个物体A、B,B的质量为m.初始时物体处于静止状态.现用竖直向上的拉力作用在物体A上,使物体A开始向上做匀加速直线运动,测得两个物体的速度υ-t图象如图乙所示,图中υ1、υ2、t1、t2已知,重力加速度为g,求:t1~t2时间内,弹簧弹性势能减少了多少?
分析 施加拉力前,两物块处于静止状态,由平衡条件求解弹簧的弹力的大小;分离时二者具有相等的速度和加速度,结合牛顿第二定律与胡克定律分别写出相应的公式;
t2时刻,物块B达到速度最大值,最后由动能定理,可求出t1~t2时间内,弹簧对B做的功,然后根据功能关系即可求出弹簧的弹性势能的变化.
解答 解:开始时A和B一起做匀加速直线运动的加速度为a=$\frac{υ_1}{t_1}$
t1时刻,A和B刚分离,对B有:F1-mg=ma
t2时刻,B速度最大,有:F2=mg
根据胡克定律,有:F1=kx1 F2=kx2
t1~t2时间内,对B,根据动能定理,有:
$\frac{1}{2}$mυ22-$\frac{1}{2}$mυ12=-mg(x1-x2)+W
得:-△EP=W=$\frac{1}{2}$mυ22-$\frac{1}{2}$mυ12+$\frac{{{m^2}g{υ_1}}}{{k{t_1}}}$
答:t1~t2时间内,弹簧弹性势能减少了$\frac{1}{2}$mυ22-$\frac{1}{2}$mυ12+$\frac{{{m^2}g{υ_1}}}{{k{t_1}}}$.
点评 施加拉力前,物块AB处于静止状态,由平衡条件可知相互作用,从受力角度看,两物体分离的条件是两物体间的正压力为0.从运动学角度看,一起运动的两物体恰好分离时,两物体在沿斜面方向上的加速度和速度仍相等.

练习册系列答案
相关题目
13.一辆汽车在公路上匀速行驶,发现前方有障碍物必须停车,开始刹车后位移变化规律为S=16t-2t 2,则下列说法中正确的是( )
| A. | 汽车停止时间为4s | |
| B. | t=6s时,汽车的位移S=24m | |
| C. | 汽车刹车位移为16m | |
| D. | 汽车初速度为32m/s,加速度为-4m/s2 |
11.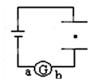 如图所示,将平行板电容器与电池相连,两板间的带电尘埃恰好处于静止状态.若将两板缓慢地错开一些,其他条件不变,则( )
如图所示,将平行板电容器与电池相连,两板间的带电尘埃恰好处于静止状态.若将两板缓慢地错开一些,其他条件不变,则( )
 如图所示,将平行板电容器与电池相连,两板间的带电尘埃恰好处于静止状态.若将两板缓慢地错开一些,其他条件不变,则( )
如图所示,将平行板电容器与电池相连,两板间的带电尘埃恰好处于静止状态.若将两板缓慢地错开一些,其他条件不变,则( )| A. | 电容器带电量变大 | B. | 电容器内部的场强变大 | ||
| C. | 灵敏电流计中有a→b的电流 | D. | 尘埃向下运动 |
18.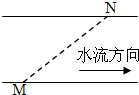 如图所示,小船沿直线MN过河,船头始终垂直于河岸.若水流速度减小,为保持航线不变,下列措施与结论正确的是( )
如图所示,小船沿直线MN过河,船头始终垂直于河岸.若水流速度减小,为保持航线不变,下列措施与结论正确的是( )
 如图所示,小船沿直线MN过河,船头始终垂直于河岸.若水流速度减小,为保持航线不变,下列措施与结论正确的是( )
如图所示,小船沿直线MN过河,船头始终垂直于河岸.若水流速度减小,为保持航线不变,下列措施与结论正确的是( )| A. | 增大船速,过河时间不变 | B. | 增大船速,过河时间缩短 | ||
| C. | 减小船速,过河时间不变 | D. | 减小船速,过河时间变长 |
8.一质点做匀加速直线运动,通过第一段8m位移所用的时间为2s,紧接着通过下一段10m位移所用时间为1s.则该质点运动的加速度大小为( )
| A. | 4m/s2 | B. | 5m/s2 | C. | 6m/s2 | D. | 7m/s2 |
12.将一个电荷量为q=10-10C的负试探电荷放在电场中A点时,测得该试探电荷受到的电场力的大小为F=10 -8N、方向向右,则A点处的电场强度为( )
| A. | 100N/C 向右 | B. | 100N/C 向左 | C. | 1×10-2C/N 向右 | D. | 1×10-2C/N 向左 |
13.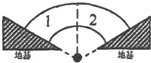 将两块相同的坚固石块垒成圆弧形的石拱,如图所示1、2石块间的接触面是竖直的且石块的外侧与地基相接触,每块石块的两个侧面间所夹的圆心角均为60°.假定石块间以及石块和地基之间的摩擦力可以忽略不计,则第1、2块石块间的作用力和石块与地基之间的作用力的大小之比为( )
将两块相同的坚固石块垒成圆弧形的石拱,如图所示1、2石块间的接触面是竖直的且石块的外侧与地基相接触,每块石块的两个侧面间所夹的圆心角均为60°.假定石块间以及石块和地基之间的摩擦力可以忽略不计,则第1、2块石块间的作用力和石块与地基之间的作用力的大小之比为( )
 将两块相同的坚固石块垒成圆弧形的石拱,如图所示1、2石块间的接触面是竖直的且石块的外侧与地基相接触,每块石块的两个侧面间所夹的圆心角均为60°.假定石块间以及石块和地基之间的摩擦力可以忽略不计,则第1、2块石块间的作用力和石块与地基之间的作用力的大小之比为( )
将两块相同的坚固石块垒成圆弧形的石拱,如图所示1、2石块间的接触面是竖直的且石块的外侧与地基相接触,每块石块的两个侧面间所夹的圆心角均为60°.假定石块间以及石块和地基之间的摩擦力可以忽略不计,则第1、2块石块间的作用力和石块与地基之间的作用力的大小之比为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\sqrt{3}$ |

