题目内容
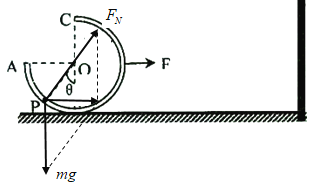
【题目】如图所示．静止在水平面上的3/4圆形（半径为R）光滑管道ABC，C为最高点，B为最低点．管道在竖直面内．管道内放一小球，小球直径略小于圆管内径且可在管道内自由移动，现用一装置将小球锁定在P点，过P点的半径0P与竖直方向的夹角为θ．现对管道施加一水平向右的恒力作用，同时解除对小球的锁定，管道沿水平面向右做匀加速运动，小球相对管道仍保持静止．经过一段时间后管道遇一障碍物突然停止运动，小球能到达管道的A点，重力加速度为g．求：
（1）恒力作用下圆形管道运动的加速度；
（2）圆形管道圆心与障碍物之间距离的可能值．
【答案】（1）a=gtanθ；（2）
+R≤s＜
+R及s=
+R
【解析】(1)设小球质量为m，对小球受力分析如图：
则
，解得： 
(2)设圆形管道在前进x后遇到障碍物突然停止前进前瞬间的速度为v，则
圆形管道停止时，小球沿管道半径方向的速度变为零，没切线方向的速度保持不变，对速度v沿切向和径向进行分解后可得，小球的速度变为
小球能运动到管道右侧圆心上方到最高点C之间的区域则可返程回到A；或小球从C点飞出做平抛运动到达A。
若小球能运动到管道右侧圆心上方到最高点C之间的区域，由机械能守恒得：
， 
联立解得： 
若小球从C点飞出做平抛运动到达A，则由机械能守恒及平抛运动规律得：
联立解得： 
圆形管道圆心与障碍物之间距离
则圆形管道圆心与障碍物之间距离的可能值为
或
练习册系列答案
相关题目
