��Ŀ����
����ͼ��ʾ��װ���У���Դ�綯��ΪE�����費�ƣ���ֵ����ΪR1��������������ֵΪR2����������е�ƽ�а������ˮƽ���ã�������Ϊd�����ڵ������е��͵�Aǡ�þ�ֹ��������ʱ�����������Ļ�ƬPλ���е�λ�ã�
��1�����ʱ�������������ĵ�ѹ��
��2������͵εĵ����Լ��͵����������q������m�ı�ֵ��
��3���ֽ������������Ļ�ƬP���е�Ѹ�����ϻ���ijλ�ã�ʹ�������ϵĵ�����仯��Q1���͵��˶�ʱ��Ϊt���ٽ���Ƭ�Ӹ�λ��Ѹ�����»�������һλ�ã�ʹ�������ϵĵ�����ֱ仯��Q2�����͵����˶���2t��ʱ�䣬ǡ�ûص�ԭ���ľ�ֹλ�ã����͵����˶�������δ�뼫��Ӵ���������������������ʱ�����������硢�ŵ�����ʱ������Բ��ƣ���Q1��Q2�ı�ֵ��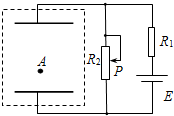
��1�����ʱ�������������ĵ�ѹ��
��2������͵εĵ����Լ��͵����������q������m�ı�ֵ��
��3���ֽ������������Ļ�ƬP���е�Ѹ�����ϻ���ijλ�ã�ʹ�������ϵĵ�����仯��Q1���͵��˶�ʱ��Ϊt���ٽ���Ƭ�Ӹ�λ��Ѹ�����»�������һλ�ã�ʹ�������ϵĵ�����ֱ仯��Q2�����͵����˶���2t��ʱ�䣬ǡ�ûص�ԭ���ľ�ֹλ�ã����͵����˶�������δ�뼫��Ӵ���������������������ʱ�����������硢�ŵ�����ʱ������Բ��ƣ���Q1��Q2�ı�ֵ��

��1����·�еĵ���I=
ƽ�а���������˵ĵ�ѹU=
=
E��
��2�������ϰ���д���磬�͵δ��ھ�ֹ״̬���糡�����ϣ����͵δ����磮���͵�������������F��-mg=0����
=mg������
=
��
��3����������ĵ���ΪC������ԭ�����еĵ����ΪQ���������ϵĵ����仯Q1���͵��ڵ糡�����������ٶ�Ϊ����ȼ���ֱ���˶���t��ĩ�͵ε��ٶ�Ϊv1��λ��Ϊs�����ĵ�ѹ
U1=
����ţ�ٵڶ����ɵ�
F��1-mg=ma1��
-mg=ma1
�����˶�ѧ��ʽ��s=
a1t2��v1=a1t
�������ϵĵ����ֱ仯��Q2���͵��ڵ糡���������ȼ���ֱ���˶���2t��ĩλ��Ϊ-s��
�����ĵ�ѹΪU2=
����ţ�ٵڶ����ɵ�
mg-F��2=ma2��mg-
=ma2
�����˶�ѧ��ʽ��-s=2v1t-
a2��2t��2
��ã�
=
��
�𣺣�1����ʱ�������������ĵ�ѹΪ
E����
��2���͵δ����磬�͵����������q������m�ı�ֵΪ
��
��3��Q1��Q2�ı�ֵΪ4��9��
| E | ||
R1+
|
ƽ�а���������˵ĵ�ѹU=
| ||
R1+
|
| R2 |
| 2R1+R2 |
��2�������ϰ���д���磬�͵δ��ھ�ֹ״̬���糡�����ϣ����͵δ����磮���͵�������������F��-mg=0����
| ||
(R1+
|
| q |
| m |
| gd(2R1+R2) |
| ER2 |
��3����������ĵ���ΪC������ԭ�����еĵ����ΪQ���������ϵĵ����仯Q1���͵��ڵ糡�����������ٶ�Ϊ����ȼ���ֱ���˶���t��ĩ�͵ε��ٶ�Ϊv1��λ��Ϊs�����ĵ�ѹ
U1=
| Q+Q1 |
| C |
����ţ�ٵڶ����ɵ�
F��1-mg=ma1��
| (Q+Q1)q |
| Cd |
�����˶�ѧ��ʽ��s=
| 1 |
| 2 |
�������ϵĵ����ֱ仯��Q2���͵��ڵ糡���������ȼ���ֱ���˶���2t��ĩλ��Ϊ-s��
�����ĵ�ѹΪU2=
| Q+Q1+Q2 |
| C |
����ţ�ٵڶ����ɵ�
mg-F��2=ma2��mg-
| (Q+Q1-Q2)q |
| Cd |
�����˶�ѧ��ʽ��-s=2v1t-
| 1 |
| 2 |
��ã�
| Q1 |
| Q2 |
| 4 |
| 9 |
�𣺣�1����ʱ�������������ĵ�ѹΪ
| R2 |
| 2R1+R2 |
��2���͵δ����磬�͵����������q������m�ı�ֵΪ
| gd(2R1+R2) |
| ER2 |
��3��Q1��Q2�ı�ֵΪ4��9��

��ϰ��ϵ�д�
�����Ŀ
 ����ͼ��ʾ��װ���У�A��B��C��DΪ�ĸ�ƽ�����ԵĽ����壬����B���C���Ͽ���С�ף��ֱ���������Դ������B��A�����ĵ�ѹΪU��C��D������ѹΪ2U���ӿ���A���F���ͷų�һ�����ٶȵĵ��ӣ������Ϊe�����ڵ��ӵ��˶���������������Щ����ȷ�ģ�������
����ͼ��ʾ��װ���У�A��B��C��DΪ�ĸ�ƽ�����ԵĽ����壬����B���C���Ͽ���С�ף��ֱ���������Դ������B��A�����ĵ�ѹΪU��C��D������ѹΪ2U���ӿ���A���F���ͷų�һ�����ٶȵĵ��ӣ������Ϊe�����ڵ��ӵ��˶���������������Щ����ȷ�ģ������� ��2011?��Ԫģ�⣩����ͼ��ʾ��װ���У���Դ�綯��ΪE�����費�ƣ���ֵ����ΪR1��������������ֵΪR2����������е�ƽ�а������ˮƽ���ã�������Ϊd�����ڵ������е��͵�Aǡ�þ�ֹ��������ʱ�����������Ļ�ƬPλ���е�λ�ã�
��2011?��Ԫģ�⣩����ͼ��ʾ��װ���У���Դ�綯��ΪE�����費�ƣ���ֵ����ΪR1��������������ֵΪR2����������е�ƽ�а������ˮƽ���ã�������Ϊd�����ڵ������е��͵�Aǡ�þ�ֹ��������ʱ�����������Ļ�ƬPλ���е�λ�ã� ����ͼ��ʾ��װ���У�ľ��B��ˮƽ����ĽӴ��ǹ⻬�ģ��ӵ�A��ˮƽ��������ľ�������ľ���ڣ����ӵ�����ľ�鵽ľ�齫����ѹ������̵�ȫ�����У�����˵����ȷ
����ͼ��ʾ��װ���У�ľ��B��ˮƽ����ĽӴ��ǹ⻬�ģ��ӵ�A��ˮƽ��������ľ�������ľ���ڣ����ӵ�����ľ�鵽ľ�齫����ѹ������̵�ȫ�����У�����˵����ȷ ��2007?���ݶ�ģ�����ڼ���̬����ԭ���������ϵ͵�״̬ԾǨʱ�ᷢ��һϵ�в�ͬƵ�ʵĹ⣬��Ϊ����ף�������ߵIJ�������������İͶ�ĩ-��²���ʽ
��2007?���ݶ�ģ�����ڼ���̬����ԭ���������ϵ͵�״̬ԾǨʱ�ᷢ��һϵ�в�ͬƵ�ʵĹ⣬��Ϊ����ף�������ߵIJ�������������İͶ�ĩ-��²���ʽ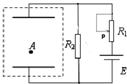 ����ͼ��ʾ��װ���У���Դ�綯��ΪE�����費�ƣ�R2Ϊ��ֵ���裬�����������Ļ�ƬPλ���е�λ��ʱ�͵�Aǡ�þ�ֹ�������罫��ƬP���»����͵ν���������
����ͼ��ʾ��װ���У���Դ�綯��ΪE�����費�ƣ�R2Ϊ��ֵ���裬�����������Ļ�ƬPλ���е�λ��ʱ�͵�Aǡ�þ�ֹ�������罫��ƬP���»����͵ν���������