题目内容
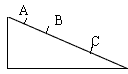
 一小球从斜面的顶端由静止以恒定的加速度滚下来,依次通过A、B、C三点,已知AB=12m,BC=32m,小球通过AB、BC所用的时间均为2s,求:
一小球从斜面的顶端由静止以恒定的加速度滚下来,依次通过A、B、C三点,已知AB=12m,BC=32m,小球通过AB、BC所用的时间均为2s,求:(1)小球下滑时加速度的大小?
(2)小球通过B点时的速度是多大?
(3)斜面上A点到顶端的长度?
分析:由于通过AB、BC所用的时间均为2s,由此可以判断B是AC的中间时刻,可以求得B的速度的大小,由匀变速直线运动的规律△x=at2 可得加速度的大小,求出A点的速度,由VA2=2aL 即可求得斜面上A点到顶端的长度.
解答:解:(1)由题意可知,A到B和B到C的时间是一样的,
由△x=at2 可得
a=
=
m/s2=5m/s2,
(2)有题意知,B是AC的中间时刻,
由匀变速直线运动的规律得,
VB=
=
=
m/s=11m/s,
(3)从A到B的过程,由速度公式可得,
VB=VA+at
所以VA=VB-at=11-5×2m/s=1m/s
斜面上A点到顶端的长度为L,则
VA2=2aL
所以L=
=
m=0.1m.
答:(1)小球下滑时加速度的大小是5m/s2;
(2)小球通过B点时的速度是11m/s;
(3)斜面上A点到顶端的长度是0.1m.
由△x=at2 可得
a=
| △x |
| t2 |
| 32-12 |
| 22 |
(2)有题意知,B是AC的中间时刻,
由匀变速直线运动的规律得,
VB=
. |
| VAC |
| AC |
| t |
| 12+32 |
| 4 |
(3)从A到B的过程,由速度公式可得,
VB=VA+at
所以VA=VB-at=11-5×2m/s=1m/s
斜面上A点到顶端的长度为L,则
VA2=2aL
所以L=
| ||
| 2a |
| 12 |
| 2×5 |
答:(1)小球下滑时加速度的大小是5m/s2;
(2)小球通过B点时的速度是11m/s;
(3)斜面上A点到顶端的长度是0.1m.
点评:本题是对匀变速直线运动的规律的考查,利用中间时刻的瞬时速度等于这个过程的平均速度,和相邻的相同时间内的位移差值定值这两个规律即可求得该题.

练习册系列答案
相关题目
 (2013?辽宁一模)足够长的光滑绝缘槽,与水平方向的夹角分别为α和β(α<β),如图所示,加垂直于纸面向里的磁场,分别将质量相等,带等量正、负电荷的小球a和b,依次从两斜面的顶端由静止释放,关于两球在槽上的运动,下列说法中正确的是( )
(2013?辽宁一模)足够长的光滑绝缘槽,与水平方向的夹角分别为α和β(α<β),如图所示,加垂直于纸面向里的磁场,分别将质量相等,带等量正、负电荷的小球a和b,依次从两斜面的顶端由静止释放,关于两球在槽上的运动,下列说法中正确的是( ) 一小球从斜面的顶端由静止以恒定的加速度滚下来,依次通过A、B、C三点,已知AB=12m,BC=32m,小球通过AB、BC所用的时间均为2s,求:
一小球从斜面的顶端由静止以恒定的加速度滚下来,依次通过A、B、C三点,已知AB=12m,BC=32m,小球通过AB、BC所用的时间均为2s,求: