题目内容
12. 如图所示.两形状完全相同的平板A.B置于光滑水平面上.质量分别为m和2m,平板B的右端固定一轻质弹簧,P点为弹簧的原长位,P点到平板B左端点Q的距离为L.物块C置于平板A的最右端,质量为m且可视为质点,平板A,物块C以相同速度v0向右运动,与静止平板B发生碰撞,碰撞时间极短,碰撞后平板A、B粘连在一起,物块C滑上平板B,运动至P点开始压缩弹簧,后被弹回并相对于平板B静止在其左端Q点.弹簧始终在弹性限度内,平板B的P点右侧部分为光滑面,P点左侧部分为粗糙面,物块C与平板B粗糙面部分之间的动摩擦因数处处相同,重力加速度为g.求:
如图所示.两形状完全相同的平板A.B置于光滑水平面上.质量分别为m和2m,平板B的右端固定一轻质弹簧,P点为弹簧的原长位,P点到平板B左端点Q的距离为L.物块C置于平板A的最右端,质量为m且可视为质点,平板A,物块C以相同速度v0向右运动,与静止平板B发生碰撞,碰撞时间极短,碰撞后平板A、B粘连在一起,物块C滑上平板B,运动至P点开始压缩弹簧,后被弹回并相对于平板B静止在其左端Q点.弹簧始终在弹性限度内,平板B的P点右侧部分为光滑面,P点左侧部分为粗糙面,物块C与平板B粗糙面部分之间的动摩擦因数处处相同,重力加速度为g.求:(1)弹簧被压缩到最短时物块C的速度大小;
(2)平板A,B在碰撞过程中损失的总动能Ek损;
(3)物块C第一次到P点时C和B的速度大小;
(4)求B的最大速度Vmax.
分析 (1)弹簧压缩至最短时,三物体的速度相等,对整体分析,根据动量守恒定律可求得C的速度;
(2)对AB分析,根据动量守恒求出碰后的速度,再由功能关系可求得损失的动能;
(3)先对物体运动的全过程分析,再对物体C第一次到P点过程分析,注意系统损失的机械能等于摩擦力与相对位移的乘积;根据能量关系及动量守恒定律列式求解;
(4)对运动过程进行分析,明确当C再次回到P点时B的速度达最大,根据(3)中求出的结果可明确最大速度.
解答 解:(1)设向右为正方向,则对整体分析可知,当弹簧压缩至最短时,ABC三者速度相同,则由动量守恒定律可知:
2mv0=(2m+2m)v1
解得:v1=$\frac{{v}_{0}}{2}$
(2)对AB碰撞过程,根据动量守恒定律有:mv0=(m+2m) v2
再由能量守恒可知,损失的总动能为:EK损=$\frac{1}{2}$mv02-$\frac{1}{2}$(m+2m)v22=$\frac{1}{3}$mv02
(3)设C停在Q点时A、B、C共同速度为v3,根据动量守恒定律有:2mv0=4mv3
解得:v3=$\frac{{v}_{0}}{2}$
对A、B、C组成的系统,从A、B碰撞结束瞬时到C停在Q点的过程,
根据功能关系有:μmg(2L)=$\frac{1}{2}$mv02+$\frac{1}{2}$(3m)v22-$\frac{1}{2}$(4m)v32
当第一次到P点时有:
2mv0=mvC+3mvB
由功能关系知:
μmgL=$\frac{1}{2}$mv02+$\frac{1}{2}$(3m)v22-$\frac{1}{2}$(3m)vB2-$\frac{1}{2}$mvC2
联立解得,vB=($\frac{1}{2}$±$\frac{\sqrt{2}}{12}$)v0;
其中($\frac{1}{2}$+$\frac{\sqrt{2}}{12}$)v0是B返回P点时的速度;应舍去;
此时C的速度vC=$\frac{{v}_{0}}{2}$+$\frac{\sqrt{2}}{4}$v0
(4)根据运动过程可知,当再次回到P点时,B的速度达最大,
由以上可知,B的最大速度为:vmax=($\frac{1}{2}$+$\frac{\sqrt{2}}{12}$)v0
答:(1)弹簧被压缩到最短时物块C的速度大小为$\frac{{v}_{0}}{2}$;
(2)平板A,B在碰撞过程中损失的总动Ek损为$\frac{1}{3}$mv02
(3)物块C第一次到P点时C和B的速度大小分别为$\frac{{v}_{0}}{2}$+$\frac{\sqrt{2}}{4}$v0和($\frac{1}{2}$±$\frac{\sqrt{2}}{12}$)v0
(4)求B的最大速度Vmax为($\frac{1}{2}$+$\frac{\sqrt{2}}{12}$)v0
点评 本题考查动量守恒定律的应用,要注意正确设定正方向,根据题意选择研究对象,明确动量守恒及功能关系的应用即可正确求解;但此题过程稍复杂,对学生分析问题能力要求较高.

 如图所示,在水平面上固定着四个完全相同的木块,一粒子弹以水平速度v射入.若子弹在木块中做匀减速直线运动,当穿透第四个木块(即D位置)时速度恰好为零,下列说法正确的是( )
如图所示,在水平面上固定着四个完全相同的木块,一粒子弹以水平速度v射入.若子弹在木块中做匀减速直线运动,当穿透第四个木块(即D位置)时速度恰好为零,下列说法正确的是( )| A. | 子弹从O 运动到D全过程的平均速度小于B点的瞬时速度 | |
| B. | 子弹通过每一部分时,其速度变化量 vA-vo=vB-vA=vC-vB=vD-vC相同 | |
| C. | 子弹到达各点的速率:v:vA:vB:vC=2:$\sqrt{3}$:$\sqrt{2}$:1 | |
| D. | 子弹从进入木块到达各点经历的时间tA:tB:tC:tD=1:$\sqrt{2}$:$\sqrt{3}$:2 |
| A. | 导体中有自由电子就有电流 | |
| B. | 导体中之所以有恒定电流,是由于导体中自由电荷在做匀速直线运动 | |
| C. | 氢原子的核外电子绕核高速旋转,因而形成与电子运行方向相同的电流 | |
| D. | 以上说法都不正确 |
| A. | 机械能一定减少 | B. | 机械能一定增加 | ||
| C. | 机械能一定不变 | D. | 无法判断机械能如何变化 |
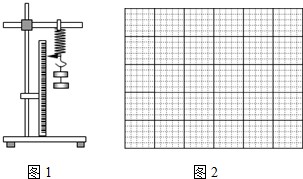
现在测得在挂钩上挂上一定数量钩码时指针在刻度尺上的读数如下表:
| 钩码数n | 0 | 1 | 2 | 3 | 4 | 5 |
| 刻度尺读数xn/cm | 2.62 | 4.17 | 5.70 | 7.22 | 8.84 | 10.43 |
(1)请根据表格数据在坐标纸中如图2作出n-xn图线,根据图线求出弹簧的劲度系数k=31N/m.(结果保留两位有效数字)
(2)考虑到弹簧自身的重力,上述测量的劲度系数等于(选填“大于”、“小于”或“等于”)真实值.
 如图所示,质量为m1=0.6kg的工件1与质量为m2=0.2kg的工件2靠在一起(并不栓接)置于粗糙水平地面上,工件1的上表面AB是一倾角为θ=37°的光滑斜面;工件2的上表面CD为一长度为L=0.5m的粗糙水平面,CD与AB相交于B(C)点且与B在同一水平面上,两工件位于同一竖直平面内,与水平地面间的动摩擦因数均为μ1=0.5,P点为AB上的一个确定点,质量M=0.2kg、可视为质点的物块与CD间的动摩擦因数为μ2=0.4,回答下列问题:(取g=10m/s2,sin37°=0.6)
如图所示,质量为m1=0.6kg的工件1与质量为m2=0.2kg的工件2靠在一起(并不栓接)置于粗糙水平地面上,工件1的上表面AB是一倾角为θ=37°的光滑斜面;工件2的上表面CD为一长度为L=0.5m的粗糙水平面,CD与AB相交于B(C)点且与B在同一水平面上,两工件位于同一竖直平面内,与水平地面间的动摩擦因数均为μ1=0.5,P点为AB上的一个确定点,质量M=0.2kg、可视为质点的物块与CD间的动摩擦因数为μ2=0.4,回答下列问题:(取g=10m/s2,sin37°=0.6)