题目内容
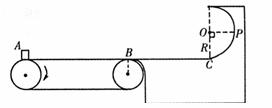
如图所示,水平传送带AB为L=21m,以6m/s顺时针匀速转动,台面传送带平滑连接于B点,半圆形光滑轨道半径R=1.25m,与水平台面相切于C点, BC长S=5.5m,一质量为m=1kg的小物块(可视为质点),从A点无初速释放,物块与带及台面间的动摩擦因数![]()
(1)求物块从A点一直向右运动到C点所用时间。
(2)试分析物块能否越来圆心O等高的P点 ,若能,物块做斜抛还是平抛;若不能,最终将停在离C点多远处?
(1)开始物块在传送带上做匀加速运动,由牛顿第二定律:
![]() ①
①
设经时间t1达到与带同速,此时物块对地面前进![]() ②
②
![]() ③
③
得t1=6s x=18m,因x=18m<21m,故后段在带上匀速用时t2
![]() t2=0.5s ④
t2=0.5s ④
从B至C过程减速运动用时t3,到达C点速度为v,
由动能定理 ![]() ⑤
⑤
而![]() ⑥
⑥
解得:![]() ⑦
⑦
故从A点一直向右运动到C点的时间为![]() ⑧
⑧
(2)设物块不能越过P点,由机械能守恒定律:![]() ⑨
⑨
解得h=1.25m,因h=R,故物块不能越过P点 ⑩
物体将沿圆周返回C点,在BC上减速后冲上传送带再返回,返回B时动能同冲上B时一样,物块从第一次返回C至停止运动的过程,动能减少在BC之间的往复运动上
对该过程由功能关系:![]()
故物体停在距C点1.5m处。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
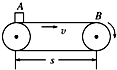 如图所示,水平传送带长为s,以速度v始终保持匀速运动,质量为m的货物无初速放到A点,货物运动到B点时恰达到速度v,货物与皮带间的动摩擦因数为μ,当货物从A点运动到B点的过程中,以下说法正确的是( )
如图所示,水平传送带长为s,以速度v始终保持匀速运动,质量为m的货物无初速放到A点,货物运动到B点时恰达到速度v,货物与皮带间的动摩擦因数为μ,当货物从A点运动到B点的过程中,以下说法正确的是( )A、摩擦力对物体做功为
| ||
| B、摩擦力对物体做功为μmgs | ||
| C、传送带克服摩擦力做功为μmgs | ||
| D、因摩擦而生的热能为2μmgs |
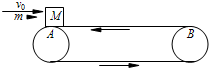 (2007?淮安模拟)如图所示,水平传送带AB长l=8.3m,质量为M=1kg的木块随传送带一起以v1=2m/s的速度向左匀速运动(传送带的传送速度恒定),木块与传送带间的动摩擦因数μ=0.5.当木块运动至最左端A点时,一颗质量为m=20g的子弹以v0=300m/s水平向右的速度正对射入木块并穿出,穿出速度v=50m/s,以后每隔1s就有一颗子弹射向木块,设子弹射穿木块的时间极短,且每次射入点各不相同,g取10m/s2.求:
(2007?淮安模拟)如图所示,水平传送带AB长l=8.3m,质量为M=1kg的木块随传送带一起以v1=2m/s的速度向左匀速运动(传送带的传送速度恒定),木块与传送带间的动摩擦因数μ=0.5.当木块运动至最左端A点时,一颗质量为m=20g的子弹以v0=300m/s水平向右的速度正对射入木块并穿出,穿出速度v=50m/s,以后每隔1s就有一颗子弹射向木块,设子弹射穿木块的时间极短,且每次射入点各不相同,g取10m/s2.求: 用如图所示的水平传送带AB和斜面BC将货物运送到斜面的顶端.传送带AB的长度L=11m,上表面保持匀速向右运行,运行的速度v=12m/s.传送带B端靠近倾角θ=37?的斜面底端,斜面底端与传送带的B端之间有一段长度可以不计的小圆弧.在A、C处各有一个机器人,A处机器人每隔△t=1.0s将一个质量m=10kg的货物箱(可视为质点)轻放在传送带A端,货物箱经传送带和斜面后到达斜面顶端的C点时速度恰好为零,C点处机器人立刻将货物箱搬走.已知斜面BC的长度s=5.0m,传送带与货物箱之间的动摩擦因数μ0=0.55,货物箱由传送带的右端到斜面底端的过程中速度大小损失原来的
用如图所示的水平传送带AB和斜面BC将货物运送到斜面的顶端.传送带AB的长度L=11m,上表面保持匀速向右运行,运行的速度v=12m/s.传送带B端靠近倾角θ=37?的斜面底端,斜面底端与传送带的B端之间有一段长度可以不计的小圆弧.在A、C处各有一个机器人,A处机器人每隔△t=1.0s将一个质量m=10kg的货物箱(可视为质点)轻放在传送带A端,货物箱经传送带和斜面后到达斜面顶端的C点时速度恰好为零,C点处机器人立刻将货物箱搬走.已知斜面BC的长度s=5.0m,传送带与货物箱之间的动摩擦因数μ0=0.55,货物箱由传送带的右端到斜面底端的过程中速度大小损失原来的 如图所示,水平传送带长为s,以速度v始终保持匀速运动,把质量为m的货物放到A点,货物与皮带间的动摩擦因数为μ,当货物从A点运动到B点的过程中,摩擦力对货物做的功可能( )
如图所示,水平传送带长为s,以速度v始终保持匀速运动,把质量为m的货物放到A点,货物与皮带间的动摩擦因数为μ,当货物从A点运动到B点的过程中,摩擦力对货物做的功可能( ) 如图所示,水平传送带以恒定速度5m/s沿图示方向运动,地面上PQ区间有垂直纸面向里的匀强磁场,B=1T,一质量为0.01kg的带正电0.05C的小物体从磁场左方某处无初速释放到传送带上,若物体与传送带间的动摩擦因数μ=0.2,那么,欲使小物体能匀速通过磁场区域,它释放时离磁场左边界P的距离应为多大?(g取10m/s2)
如图所示,水平传送带以恒定速度5m/s沿图示方向运动,地面上PQ区间有垂直纸面向里的匀强磁场,B=1T,一质量为0.01kg的带正电0.05C的小物体从磁场左方某处无初速释放到传送带上,若物体与传送带间的动摩擦因数μ=0.2,那么,欲使小物体能匀速通过磁场区域,它释放时离磁场左边界P的距离应为多大?(g取10m/s2)