题目内容
【题目】如图所示,在第一象限内有沿y轴负方向的电场强度大小为E的匀强电场.在第二象限中,半径为R的圆形区域内存在垂直纸面向外的匀强磁场,圆形区域与x、y轴分别相切于A、C两点.在A点正下方有一个粒子源P,P可以向x轴上方各个方向射出速度大小均为v0、质量为m、电荷量为+q的带电粒子(重力不计,不计粒子间的相互作用),其中沿y轴正向射出的带电粒子刚好从C点垂直于y轴进入电场.
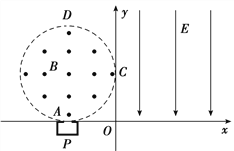
(1)求匀强磁场的磁感应强度大小B.
(2)求带电粒子到达x轴时的横坐标范围和带电粒子到达x轴前运动时间的范围.
(3)如果将第一象限内的电场方向改为沿x轴负方向,分析带电粒子将从何处离开磁场,可以不写出过程.
【答案】(1)![]() (2)x的范围
(2)x的范围![]() ,t的范围
,t的范围![]() (3)从A点正上方的D点离开磁场
(3)从A点正上方的D点离开磁场
【解析】试题分析:由题设条件,从A点沿y轴正方向射出的带电粒子刚好从C点垂直于y轴进入电场,由几何关系知道它做匀速圆周运动的半径为R,再由洛仑兹力提供向心力可以求得磁感应强度的大小;由于所有粒子做匀速圆周运动的半径等于磁场圆的半径,可以证明:沿不同方向进入磁场的带电粒子离开磁场时方向均沿x轴正方向进入电场,之后做类平抛运动,显然运动时间最长的带电粒子是从D点水平射出的粒子,由类平抛运动运动规律就能求出打在x轴的最远点;若将第一象限的电场改为沿x轴负方向,则粒子从磁场水平射出后做匀减速直线运动至速度为零,再沿x轴负方向做匀加速直线运动进入磁场做匀速圆周运动,由于速度方向反向,则粒子所受洛仑兹力反向,最后从D点射出磁场.
(1)带电粒子在磁场中做匀速圆周运动,从A点运动到C点的过程中带电粒子的运动轨迹为![]() 个圆弧,轨迹半径r=R
个圆弧,轨迹半径r=R
由![]() ,得
,得![]()
(2)沿不同方向进入磁场的带电粒子离开磁场时的速度大小均为v0,方向均平行于x轴,其临界状态为粒子从D点沿x轴正方向离开磁场
分析粒子从D点离开磁场的情况,粒子在磁场中运动时间为![]() ,
,![]() 得
得![]()
从D点平行于x轴运动至y轴的时间![]()
在第一象限内运动过程中,粒子做类平抛运动,设运动时间为t3,则![]() ,
,![]() ,
,![]()
解得![]() ,
,![]()
则![]()
带电粒子到达x轴时的横坐标范围为 ![]()
到达x轴前运动时间的范围 ![]()
(3)将第一象限内的电场方向改为沿x轴负向时,带电粒子将从A点正上方的D点离开磁场。
【点睛】本题的关键点是带电粒子做匀速圆周运动的半径恰与磁场圆的半径相等,可以证明两圆心与两交点构成菱形,所以两对边平行,从而离开磁场中速度方向水平向右.这也是磁聚焦的大原理。
【题型】解答题
【结束】
94
【题目】下列说法正确的是________.
A.在完全失重的情况下,气体的压强为零
B.液体表面张力产生的原因是液体表面层分子较稀疏,分子间的引力大于斥力
C.当两分子间距离大于平衡位置的间距时,分子间的距离越大,分子势能越小
D.水中气泡上浮过程中,气泡中的气体在单位时间内与气泡壁单位面积碰撞的分子数减小
E.不可能利用高科技手段将散失在环境中的内能重新收集起来加以利用而不引起其他变化
【答案】BDE
【解析】根据气体压强的产生原因,在完全失重的情况下,气体的压强并不为零,A错误;液体表面张力产生的原因是液体表面层分子较稀疏,分子间的引力大于斥力,B正确;当两分子间距离大于平衡位置的间距时,分子间的距离越大,分子势能越大,C错误;气泡在水中上浮过程中,体积增大,温度基本不变,压强减小,根据气体压强的微观解释可知,D正确;根据热力学第二定律,可知不可能将散失在环境中的内能重新收集起来加以利用而不引起其他变化,E正确.

 天天向上口算本系列答案
天天向上口算本系列答案