题目内容
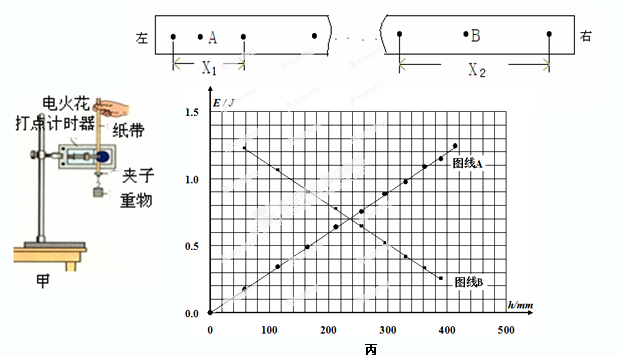
在验证牛顿第二定律的实验中，采用如图所示的实验装置。在探究加速度a与所受外力F的关系实验过程，某小组得到了如图所示的纸带（两计数点间还有四个点没有画出），已知打点计时器采用的是频率为50HZ的交流电，则两计数点间的时间间隔为 s，根据纸带可求出小车的加速度大小为 m/s2。（保留两位有效数字）
由于他们操作不当得到的a－F关系图象如图所示，其原因是：________________________________
0.1（2分）；0.50（3分）；没有平衡摩擦力（或木板的倾角过小）（2分）。
解析试题分析：由于实验时使用的是频率为50HZ的交流电，故每两个点间的时间间隔是0.02s，又因为两计数点间还有四个点没有画出，故两计数点间的时间间隔为0.02s×5=0.1s；我们可以利用逐差法计算加速度的大小，即a=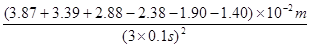
=0.50m/s2；又由a－F关系图象可知，只有当拉力为一定时，小车才产生加速度，所以产生这种现象的原因是没有平衡摩擦力（或木板的倾角过小）。
考点：通过纸带计算加速度，对牛顿第二定律实验图像的分析。
口算题卡北京妇女儿童出版社系列答案研究小车匀变速直线运动的实验装置如图所示其中斜面倾角θ可调，打点计时器的工作频率为50 Hz，纸带上计数点的间距如图所示，其中每相邻两点之间还有4个记录点未画出。
部分实验步骤如下：
| A．测量完毕，关闭电源，取出纸带 |
| B．接通电源，待打点计时器工作稳定后放开小车 |
| C．将小车停靠在打点计时器附近，小车尾部与纸带相连 |
| D．把打点计时器固定在平板上，让纸穿过限位孔，上述实验步骤的正确顺序是：（用字母填写） |
计数点5对应的瞬时速度大小计算式为v5= 。（用字母表示）；
为了充分利用记录数据，减小误差，小车加速度大小的计算式应为a= （用字母表示）
图线，如图丙。由图线C可知电池C的电动势E= ；内阻r= （计算结果保留两位有效数字）；内阻测量值与真实值相比 (选填“偏大”、 “偏小”)伽利略的自由落体实验和加速度实验均被选为最美的实验。在加速度实验中，伽利略将光滑直木板槽倾斜固定，让铜球从木槽顶端沿斜面由静止滑下，并用水钟测量铜球每次下滑的时间，研究铜球的运动路程和时间的关系。亚里士多德曾预言铜球的运动速度是不变的，伽利略却证明铜球运动的路程与时间的平方成正比。请将亚里士多德的预言和伽利略的结论分别用公式表示（其中路程用s，速度用v，加速度用a，时间用t表示）。
①亚里士多德的预言： ；
②伽利略的结论： ；
伽利略的实验之所以成功，主要原因是抓住了主要因素，而忽略了次要因素。你认为他在加速度实验中，伽利略选用光滑直木槽和铜球进行实验来研究铜球的运动，是为了减小铜球运动过程中的摩擦阻力这一次要因素，同时抓住了 这一主要因素。若将此实验结论做合理外推，即可适用于自由落体运动，其原因是在实验误差范围内，铜球运动的加速度 （填序号即可）。
| A．与铜球质量成正比 |
| B．只与斜面倾角有关 |
| C．与斜面倾角无关 |
| D．与铜球质量和斜面倾角都有关 |
