题目内容
13.如图1所示,为“探究加速度与力、质量的关系”实验装置及数字化信息系统获得了小车加速度a与钩码的质量及小车和砝码的质量对应关系图.钩码的质量为m1,小车和砝码的质量为m2,重力加速度为g.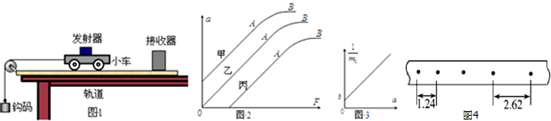
(1)下列说法正确的是D.
A.每次在小车上加减砝码时,应重新平衡摩擦力
B.实验时若用打点计时器应先释放小车后接通电源
C.本实验m2应远小于m1
D.在用图象探究加速度与质量关系时,应作a-$\frac{1}{{m}_{2}}$图象
(2)实验时,某同学由于疏忽,遗漏了平衡摩擦力这一步骤,测得F=m1g,作出a-F图象,他可能作出图2中丙 (选填“甲”、“乙”、“丙”)图线.此图线的AB段明显偏离直线,造成此误差的主要原因是C.
A.小车与轨道之间存在摩擦 B.导轨保持了水平状态
C.所挂钩码的总质量太大 D.所用小车的质量太大
(3)实验时,某同学遗漏了平衡摩擦力这一步骤,若轨道水平,他测量得到的$\frac{1}{{m}_{2}}$-a图象,如图3.设图中直线的斜率为k,在纵轴上的截距为b,则小车与木板间的动摩擦因数μ=$\frac{b}{gk}$,钩码的质量m1=$\frac{1}{gk}$.
(4)实验中打出的纸带如图4所示.相邻计数点间的时间是0.1s,图中长度单位是cm,由此可以算出小车运动的加速度是0.46m/s2.
分析 (1)根据实验的原理以及注意事项确定正确的选项.
(2)如果没有平衡摩擦力的话,就会出现当有拉力时,物体不动的情况.得出图象弯曲的原因是:未满足沙和沙桶质量远小于小车的质量.
(3)根据牛顿第二定律,列出小车的滑动摩擦力大小,然后结合图象的斜率与截距,可以得出结论.
(4)根据连续相等时间内的位移之差是一恒量求出加速度.
解答 解:(1)A、平衡摩擦力,假设木板倾角为θ,则有:f=mgsinθ=μmgcosθ,m约掉了,每次在小车上加减砝码时,不需要重新平衡摩擦力.故A错误.
B、实验时应先接通电源后释放小车,故B错误.
C、在该实验中,为了使钩码的重力近似等于绳子的拉力,则要求钩码的质量m1远小于小车的质量m2,故C错误;
D、F=ma,所以:a=$\frac{F}{m}$,所以在用图象探究小车的加速度与质量的关系时,通常作a-$\frac{1}{{m}_{2}}$图象,故D正确;
故选:D
(2)遗漏了平衡摩擦力这一步骤,就会出现当有拉力时,物体不动的情况,说明没有平衡摩擦力或平衡不够.故可能作出图2中丙.
此图线的AB段明显偏离直线,造成此误差的主要原因是砝码盘和砝码的总质量太大,没有远小于小车和砝码的质量,故C正确,
故选:C.
(3)实验时,某同学遗漏了平衡摩擦力这一步骤,
根据牛顿第二定律得:
F-μm2g=m2a
m1g-F=m1a
$\frac{1}{{m}_{2}}=\frac{a}{F}+\frac{μg}{F}$
设图中直线的斜率为k,在纵轴上的截距为b,
所以k=$\frac{1}{F}$,$\frac{μg}{F}$=b,
解得:μ=$\frac{b}{gk}$,钩码的质量m1=$\frac{1}{gk}$.
(4)根据匀变速直线的推论:s4-s1=3aT2
a=$\frac{0.0262-0.0124}{0.03}$=0.46m/s2
故答案为:(1)D;(2)丙,C; (3)$\frac{b}{gk}$,$\frac{1}{gk}$;(4)0.46
点评 本题考察的比较综合,需要学生对这一实验掌握的非常熟,理解的比较深刻才不会出错,知道a-F图的斜率等于小车质量的倒数,难度适中.要提高应用匀变速直线的规律以及推论解答实验问题的能力,在平时练习中要加强基础知识的理解与应用.

| A. | 磁带式录音机 | B. | 计算机硬盘 | C. | 白炽灯 | D. | 磁卡 |
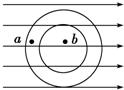 如图所示,在一电场强度为E的匀强电场中放一金属空心导体,图中a、b分别为金属导体内部与空腔中的点,导体处于静电平衡状态(各处电场为0,处于等势体),则( )
如图所示,在一电场强度为E的匀强电场中放一金属空心导体,图中a、b分别为金属导体内部与空腔中的点,导体处于静电平衡状态(各处电场为0,处于等势体),则( )| A. | a、b两点的电场强度都为零 | B. | a点电场强度为零,b点不为零 | ||
| C. | a点电势高于b点电势 | D. | a、b两点电场强度均不为零 |
 已知一个均匀带电的薄球壳上的电荷在壳内任意一点产生的电场强度均为零,在壳外某点产生的电场强度,等同于把壳上电量全部集中在球心处的点电荷所产生的电场强度,即:E=$\left\{\begin{array}{l}{0,(r<R)}\\{k\frac{Q}{{r}^{2}},(r>R)}\end{array}\right.$,式中R为球壳的半径,r为某点到球壳球心的距离,Q为球壳所带的电荷量,k为静电力常量.在真空中有一半径为R、电荷量为-Q的均匀带负电薄球壳,球心位置O固定,P为球壳外一点,M为球壳内一点,如图所示,以无穷远处为电势零点,关于P、M两点的电场强度和电势,下列说法中正确的是( )
已知一个均匀带电的薄球壳上的电荷在壳内任意一点产生的电场强度均为零,在壳外某点产生的电场强度,等同于把壳上电量全部集中在球心处的点电荷所产生的电场强度,即:E=$\left\{\begin{array}{l}{0,(r<R)}\\{k\frac{Q}{{r}^{2}},(r>R)}\end{array}\right.$,式中R为球壳的半径,r为某点到球壳球心的距离,Q为球壳所带的电荷量,k为静电力常量.在真空中有一半径为R、电荷量为-Q的均匀带负电薄球壳,球心位置O固定,P为球壳外一点,M为球壳内一点,如图所示,以无穷远处为电势零点,关于P、M两点的电场强度和电势,下列说法中正确的是( )| A. | 若Q不变,M点的位置也不变,而令R变小(M点仍在壳内),则M点的电势降低 | |
| B. | 若Q不变,M点的位置也不变,而令R变小(M点仍在壳内),则M点的场强不变 | |
| C. | 若Q不变,P点的位置也不变,而令R变小,则P点的场强不变 | |
| D. | 若Q不变,P点的位置也不变,而令R变小,则P点的电势升高 |
 如图所示,变压器的输入电压U一定,两个副线圈的匝数是n2和n3.当把电热器接a、b,让c、d 空载时,电流表读数是I2;当把同一电热器接c、d,而a、b空载时,电流表读数是I3,则I2:I3等于( )
如图所示,变压器的输入电压U一定,两个副线圈的匝数是n2和n3.当把电热器接a、b,让c、d 空载时,电流表读数是I2;当把同一电热器接c、d,而a、b空载时,电流表读数是I3,则I2:I3等于( )| A. | n2:n3 | B. | n3:n2 | C. | n22:n32 | D. | n32:n22 |
| A. | 伽利略发现地月间的引力满足距离平方反比规律 | |
| B. | 卡文迪许通过实验测出了万有引力常量 | |
| C. | 用比值法来描述加速度这个物理量,其表达式a=$\frac{F}{m}$ | |
| D. | 将物体视为质点,采用了等效替代法 |
 小明同学用图(1)所示的实验装置验证规律:物体质量一定,其加速度与所受合力成正比.
小明同学用图(1)所示的实验装置验证规律:物体质量一定,其加速度与所受合力成正比.

 如图所示,在x轴上,坐标为+1的点上固定一个电量为+4Q的点电荷,在坐标原点O处固定一电量为-Q的点电荷.那么,在x坐标上,电场强度方向沿-x方向的点所在的区域是0<x<1m和x<-1m.
如图所示,在x轴上,坐标为+1的点上固定一个电量为+4Q的点电荷,在坐标原点O处固定一电量为-Q的点电荷.那么,在x坐标上,电场强度方向沿-x方向的点所在的区域是0<x<1m和x<-1m.