题目内容
6．
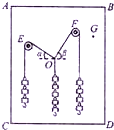某同学用如图所示的装置，探究共点力合成的规律．ABCD为竖直平板，E、F两处固定了摩擦不计的轻质滑轮，滑轮的轴保持水平，所用绳子的质量可不计．第一次实验，当装置平衡时，记下绳子的结点D和三段绳子拉力的方向和对应钩码的数目，数据如图所示，如果“力的平行四边形定则”成立，则$\frac{sinβ}{sinα}$=$\frac{4}{3}$；第二次实验，仅把右侧滑轮F的位置移动到图中的G点，待稳定后，∠EOF将不变（选填“变大”、“变小”或“不变”）．
分析 稳定后，O点处于平衡状态，所受三个力的合力为零，即任何两个力的合力与另外一个力等大反向，根据平衡条件和平行四边形定则可正确解答．
解答 解：第一次实验，当装置平衡时，记下绳子的结点D和三段绳子拉力的方向和对应钩码的数目，
根据O点处于平衡状态，正交分解有：
竖直方向：3mgsinα+4mgsinβ=5mg ①
水平方向：3mgcosα=4mgcosβ ②
联立①②解得：$\frac{sinβ}{sinα}$=$\frac{4}{3}$．
以O点为研究对象，受到三个力的作用，由于钩码个数不变，因此三个力的大小不变，O点所受竖直方向的拉力大小方向不变，即EO，FO两绳子拉力的合力大小方向不变，根据平行四边形定则可知，二力的大小不变，其合力的大小方向不变，则该二力的夹角不变，故∠EOF不变；
故答案为：方向，$\frac{4}{3}$，不变．
点评 掌握三力平衡的条件，理解平行四边形定则，同时验证平行四边形定则是从力的图示角度去作图分析．
练习册系列答案
相关题目
16．在静电场中，一个负电荷 受到非静电力作用由一条电场线上的A点移到B点，以下说法中正确的是（ ）
| A． | 非静电力和电场力对电荷做功之和等于电荷电势能增加量和动能增加量之和 | |
| B． | 非静电力做功等于电荷电势能和动能的增加量之和 | |
| C． | 电荷克服电场力做功等于电荷电势能的增加量 | |
| D． | 非静电力和电场力做功之和等于电荷动能增加量 |
17．竖直升空的火箭，其速度-时间图象如图所示，由图可知以下说法正确的是（ ）
| A． | 火箭在40s时速度方向发生变化 | B． | 火箭经过40s到达最高点 | ||
| C． | 火箭经过120s落回地面 | D． | 火箭上升的最大高度为48000m |
1．放射性元素${\;}_{b}^{a}$X的衰变反应是：${\;}_{b}^{a}$X→${\;}_{d}^{c}$Y+N，其中N是未知的射线，则下列说法正确的是（ ）
| A． | 若此衰变为β衰变，则b=d+1 | |
| B． | 若此衰变为α衰变，则a=c+4 | |
| C． | 若放射性元素${\;}_{b}^{a}$X经过6 h还剩下$\frac{1}{8}$没有衰变，则它的半衰期为2 h | |
| D． | 用射线N照射锌板一定可使锌板带电 |
2014年8月20日，日本广岛县发生特大泥石流灾害．一汽车停在距离小山坡底20m处，在距坡底80m的山坡处泥石流从静止以0.4m/s2的加速度匀加速倾泻而下，当泥石流滑到坡底时，司机才突然发现并启动汽车，假设司机（反应时间为1s）以2m/s2的加速度匀加速启动汽车且一直做匀加速直线运动（如图所示），而泥石流到达坡底后速率不变且在水平面的运动近似看成匀速直线运动．问：汽车司机能否安全脱离？
在做“研究平抛物体的运动”的实验中，为了确定小球在不同时刻在空中所通过的位置，实验时用了如图所示的装置．先将斜槽轨道的末端调整水平，在一块平整的木板表面钉上白纸和复写纸．将该木板竖直立于水平地面上，使一小球从斜槽上紧靠挡板处由静止释放，小球撞到木板并在白纸上留下痕迹A；将木板向远离槽口平移距离x，再使小球从斜槽上紧靠挡板处由静止释放，小球撞在木板上得到痕迹B；又将木板再向远离槽口平移距离x，小球再从斜槽上紧靠挡板处由静止释放，再得到痕迹C．若测得木板每次移动距离x=10.00cm，A、B间距离y1=5.02cm，B、C间距离y2=14.82cm．请回答以下问题（g=9.80m/s2）