题目内容
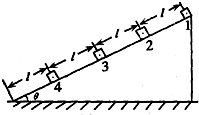 (2005?海门市模拟)4个相同的木块,每块的质量都是m,每块均可以看作质点,放置在倾角为θ的斜面上,相邻两木块间的距离为l,最下端的木块距底端也是l,木块与斜面间的动摩擦因数为μ,如图所示,在开始时刻,第一个木块以初速度v0沿斜面下滑,其余所有木块都静止.由于第一个木块的下滑将依次引起一系列的碰撞,每次发生碰撞时间都很短,在发生碰撞后,发生碰撞的木块都粘在一起运动,直到最后第4个木块到达斜面底端时,刚好停在底端.求:
(2005?海门市模拟)4个相同的木块,每块的质量都是m,每块均可以看作质点,放置在倾角为θ的斜面上,相邻两木块间的距离为l,最下端的木块距底端也是l,木块与斜面间的动摩擦因数为μ,如图所示,在开始时刻,第一个木块以初速度v0沿斜面下滑,其余所有木块都静止.由于第一个木块的下滑将依次引起一系列的碰撞,每次发生碰撞时间都很短,在发生碰撞后,发生碰撞的木块都粘在一起运动,直到最后第4个木块到达斜面底端时,刚好停在底端.求:(1)第一次碰撞前第一个木块的动能E1.
(2)第一次碰撞时系统损失的机械能△E1.
(3)在整个过程中由于碰撞而损失的总机械能△E.
分析:(1)对第一个木块下滑的过程中,由动能定理可求出碰撞前第一个木块的动能E1.
(2)由动量守恒可求出木块1碰撞后的速度大小;碰撞前因摩擦力做功,导致小木块机械能损失;再求出碰撞后小木块动能的减小导致机械能损失;从而两者之和即为从第一个小木块开始运动到第一次碰撞后系统损失的机械能;
(3)通过力做功表达式求出碰撞整个过程中,重力、摩擦力做功;再根据功能关系可求出在碰撞中总机械能损失.
(2)由动量守恒可求出木块1碰撞后的速度大小;碰撞前因摩擦力做功,导致小木块机械能损失;再求出碰撞后小木块动能的减小导致机械能损失;从而两者之和即为从第一个小木块开始运动到第一次碰撞后系统损失的机械能;
(3)通过力做功表达式求出碰撞整个过程中,重力、摩擦力做功;再根据功能关系可求出在碰撞中总机械能损失.
解答:解:(1)对第一个木块下滑的过程中,由动能定理得
mglsinθ-μmglcosθ=E1-
mv02?
即 E1=mglsinθ-μmglcosθ+
mv02
(2)第一个木块与第二个木块碰撞过程中,由动量守恒定律近似得
mv1=2mv1′,即v1′=
v1
E1′=
×2mv1′2,
则得△E1=E1-E1′=
E1=
(mglsinθ-μmglcosθ+
mv02)
(3)由总能量守恒可得:
mglsinθ+2mglsinθ+3mglsinθ+4mglsinθ+
mv02=△E+μmglcosθ+2μmglcosθ+3μmglcosθ+4μmglcosθ
即△E=10mgl(sinθ-μcosθ)+
mv02.?
答:
(1)第一次碰撞前第一个木块的动能E1是mglsinθ-μmglcosθ+
mv02.
(2)第一次碰撞时系统损失的机械能△E1是
(mglsinθ-μmglcosθ+
mv02).
(3)在整个过程中由于碰撞而损失的总机械能△E是10mgl(sinθ-μcosθ)+
mv02.
mglsinθ-μmglcosθ=E1-
| 1 |
| 2 |
即 E1=mglsinθ-μmglcosθ+
| 1 |
| 2 |
(2)第一个木块与第二个木块碰撞过程中,由动量守恒定律近似得
mv1=2mv1′,即v1′=
| 1 |
| 2 |
E1′=
| 1 |
| 2 |
则得△E1=E1-E1′=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(3)由总能量守恒可得:
mglsinθ+2mglsinθ+3mglsinθ+4mglsinθ+
| 1 |
| 2 |
即△E=10mgl(sinθ-μcosθ)+
| 1 |
| 2 |
答:
(1)第一次碰撞前第一个木块的动能E1是mglsinθ-μmglcosθ+
| 1 |
| 2 |
(2)第一次碰撞时系统损失的机械能△E1是
| 1 |
| 2 |
| 1 |
| 2 |
(3)在整个过程中由于碰撞而损失的总机械能△E是10mgl(sinθ-μcosθ)+
| 1 |
| 2 |
点评:本题是力学综合题,考查动能定理、动量守恒定律、功的公式、功与能关系等规律,同时动量守恒定律注意矢量性及功的正负.

练习册系列答案
相关题目
 (2005?海门市模拟)某同学利用焊有细钢针的音叉(固有频率f0)、熏有煤油灯烟灰的均匀金属片和刻度尺来测定重力加速度.他的实验步骤有:
(2005?海门市模拟)某同学利用焊有细钢针的音叉(固有频率f0)、熏有煤油灯烟灰的均匀金属片和刻度尺来测定重力加速度.他的实验步骤有: (2005?海门市模拟)如图所示,在光滑的桌面上叠放着一质量为mA=2.0kg的薄木板A和质量为mB=3.0kg的小金属块B,A的长度L=2.0m,B上有轻线绕过定滑轮与质量为mC=1.0kg的物块C相连,B与A之间的动摩擦因数μ=0.10,最大静摩擦力可视为等于滑动摩擦力,忽略滑轮质量及与轴间的摩擦,起始时令各物体都处于静止状态,绳被拉直,B位于A的左端(如图),然后放手,求(1)A、B的加速度;(2)经过多长时间t后B从A的右端脱离(设A的右端距滑轮足够远)(取g=10m/s2)
(2005?海门市模拟)如图所示,在光滑的桌面上叠放着一质量为mA=2.0kg的薄木板A和质量为mB=3.0kg的小金属块B,A的长度L=2.0m,B上有轻线绕过定滑轮与质量为mC=1.0kg的物块C相连,B与A之间的动摩擦因数μ=0.10,最大静摩擦力可视为等于滑动摩擦力,忽略滑轮质量及与轴间的摩擦,起始时令各物体都处于静止状态,绳被拉直,B位于A的左端(如图),然后放手,求(1)A、B的加速度;(2)经过多长时间t后B从A的右端脱离(设A的右端距滑轮足够远)(取g=10m/s2) (2005?海门市模拟)如图所示,一倾角为θ的斜面固定在地面上,现有一箱子恰好能沿此斜面匀速下滑.设箱子所受斜面的支持力为FN,滑动摩擦力为Ff,箱子与斜面间的动摩擦因数为μ,如果再向箱子内放一质量为m的重物,则箱子在斜面上( )
(2005?海门市模拟)如图所示,一倾角为θ的斜面固定在地面上,现有一箱子恰好能沿此斜面匀速下滑.设箱子所受斜面的支持力为FN,滑动摩擦力为Ff,箱子与斜面间的动摩擦因数为μ,如果再向箱子内放一质量为m的重物,则箱子在斜面上( )