Question

【题目】如图，小球a、b用等长细线悬挂于同一固定点O．让球a静止下垂，将球b向右拉起，使细线水平．从静止释放球b，两球碰后粘在一起向左摆动，此后细线与竖直方向之间的最大偏角为60°．忽略空气阻力，求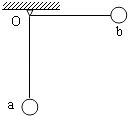

①两球a、b的质量之比；
②两球在碰撞过程中损失的机械能与球b在碰前的最大动能之比．

Answer 1

【答案】解：设a球的质量为m1，b球的质量为m2，b球下摆过程中，由动能定理得：

m2gL= m2v02﹣0，

碰撞过程动量守恒，设向左为正方向，由动量守恒定律可得：

m2v0=（m1+m2）v，

两球向左摆动过程中，由机械能守恒定律得：

（m1+m2）v2=（m1+m2）gL（1﹣cosθ），

解得： =（ ﹣1）：1=（ ﹣1）：1

两球碰撞过程中损失的机械能：

Q=m2gL﹣（m1+m2）gL（1﹣cosθ），

碰前b球的最大动能为：Eb= m2v02，

=[1﹣ （1﹣cosθ）]：1=（1﹣ ）：1=

答：①两球a、b的质量之比为（ ﹣1）：1

②两球在碰撞过程中损失的机械能与球b在碰前的最大动能之比为（2﹣ ）：2．

【解析】（1）b球下摆过程中，只有重力做功，由动能定理可以求出碰前b球的速度；碰撞过程中动量守恒，由动量守恒定律列方程，两球向左摆动过程中，机械能守恒，由机械能守恒定律或动能定理列方程，解方程组可以求出两球质量之比．（2）求出碰撞过程中机械能的损失，求出碰前b求的动能，然后求出能量之比．
【考点精析】解答此题的关键在于理解功能关系的相关知识，掌握当只有重力（或弹簧弹力）做功时，物体的机械能守恒；重力对物体做的功等于物体重力势能的减少:W G =E p1 -E p2；合外力对物体所做的功等于物体动能的变化:W 合 =E k2 -E k1 （动能定理）；除了重力（或弹簧弹力）之外的力对物体所做的功等于物体机械能的变化:W F =E 2 -E 1，以及对动量守恒定律的理解，了解动量守恒定律成立的条件：系统不受外力或系统所受外力的合力为零；系统所受的外力的合力虽不为零，但系统外力比内力小得多；系统所受外力的合力虽不为零，但在某个方向上的分量为零，则在该方向上系统的总动量的分量保持不变．