题目内容
7.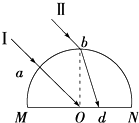 半径为R的半圆柱形玻璃砖的截面如图所示,O为圆心,光线Ⅰ沿半径方向从a点射入玻璃砖后,恰好在O点发生全反射,另一条光线Ⅱ平行于光线Ⅰ从最高点b射入玻璃砖后,在底边MN上的d点射出.若测得Od=$\frac{R}{4}$,则该玻璃砖的折射率为多少?
半径为R的半圆柱形玻璃砖的截面如图所示,O为圆心,光线Ⅰ沿半径方向从a点射入玻璃砖后,恰好在O点发生全反射,另一条光线Ⅱ平行于光线Ⅰ从最高点b射入玻璃砖后,在底边MN上的d点射出.若测得Od=$\frac{R}{4}$,则该玻璃砖的折射率为多少?
分析 根据折射率的定义公式n=$\frac{sini}{sinγ}$和全反射临界角公式sinC=$\frac{1}{n}$列式后联立求解即可.
解答 解:设光线Ⅱ的入射角和折射角分别为i和r,在△bOd中,
bd=$\sqrt{o{b}^{2}+o{d}^{2}}$=$\frac{\sqrt{17}}{4}$R,
sinr=$\frac{od}{bd}$=$\frac{\sqrt{17}}{17}$
由折射定律有n=$\frac{sini}{sinγ}$
即sini=$\frac{\sqrt{17}}{7}$n
又因为光线Ⅰ与光线Ⅱ平行,且在O点恰好发生全反射,有:
sini=$\frac{1}{n}$,
所以$\frac{\sqrt{17}}{7}$n=$\frac{1}{n}$,
从而得到:
n=$\root{4}{17}$≈2.03
答:该玻璃砖的折射率为2.03.
点评 本题是简单的几何光学问题,其基础是作出光路图,根据几何知识确定入射角与折射角,根据折射定律求解.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
18.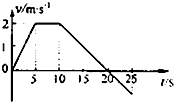 某同学站在电梯底板上,利用速度传感器和计算机研究一观光电梯升降过程中的情况,如图所示的v-t图象是计算机显示的观光电梯在某一段时间内速度变化的情况(向上为正方向).根据图象提供的信息,可以判断下列说法中正确的是( )
某同学站在电梯底板上,利用速度传感器和计算机研究一观光电梯升降过程中的情况,如图所示的v-t图象是计算机显示的观光电梯在某一段时间内速度变化的情况(向上为正方向).根据图象提供的信息,可以判断下列说法中正确的是( )
 某同学站在电梯底板上,利用速度传感器和计算机研究一观光电梯升降过程中的情况,如图所示的v-t图象是计算机显示的观光电梯在某一段时间内速度变化的情况(向上为正方向).根据图象提供的信息,可以判断下列说法中正确的是( )
某同学站在电梯底板上,利用速度传感器和计算机研究一观光电梯升降过程中的情况,如图所示的v-t图象是计算机显示的观光电梯在某一段时间内速度变化的情况(向上为正方向).根据图象提供的信息,可以判断下列说法中正确的是( )| A. | 在5s~10s内,该同学对电梯底板的压力大于他所受的重力 | |
| B. | 在0~5s内,观光电梯在加速上升,该同学处于失重状态 | |
| C. | 在10s~20s内,观光电梯在减速下降,该同学处于失重状态 | |
| D. | 在20s~25s内,观光电梯在加速下降,该同学处于失重状态 |
15.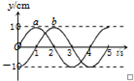 一列简谐横波沿直线由a向b传播,相距5.0m的a、b两处的 质点振动图象如图中a、b所示,则以下说法正确的是( )
一列简谐横波沿直线由a向b传播,相距5.0m的a、b两处的 质点振动图象如图中a、b所示,则以下说法正确的是( )
 一列简谐横波沿直线由a向b传播,相距5.0m的a、b两处的 质点振动图象如图中a、b所示,则以下说法正确的是( )
一列简谐横波沿直线由a向b传播,相距5.0m的a、b两处的 质点振动图象如图中a、b所示,则以下说法正确的是( )| A. | 该波的波长可能是18m | B. | 该波的波速可能是5m/s | ||
| C. | 该波的波长可能是5m | D. | 该波由a传播到b可能历时6s |
2.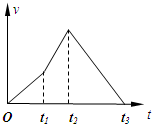 某科技兴趣小组用实验装置模拟火箭发射卫星.火箭点燃后从地面竖直升空,燃料燃尽后火箭的第一级第二级相继脱落,实验中测得卫星竖直方向的速度-时间图象如图所示,设运动中不计空气阻力,燃料燃烧时产生的推力大小恒定.下列判断正确的是( )
某科技兴趣小组用实验装置模拟火箭发射卫星.火箭点燃后从地面竖直升空,燃料燃尽后火箭的第一级第二级相继脱落,实验中测得卫星竖直方向的速度-时间图象如图所示,设运动中不计空气阻力,燃料燃烧时产生的推力大小恒定.下列判断正确的是( )
 某科技兴趣小组用实验装置模拟火箭发射卫星.火箭点燃后从地面竖直升空,燃料燃尽后火箭的第一级第二级相继脱落,实验中测得卫星竖直方向的速度-时间图象如图所示,设运动中不计空气阻力,燃料燃烧时产生的推力大小恒定.下列判断正确的是( )
某科技兴趣小组用实验装置模拟火箭发射卫星.火箭点燃后从地面竖直升空,燃料燃尽后火箭的第一级第二级相继脱落,实验中测得卫星竖直方向的速度-时间图象如图所示,设运动中不计空气阻力,燃料燃烧时产生的推力大小恒定.下列判断正确的是( )| A. | t2时刻卫星到达最高点,t3时刻卫星落回地面 | |
| B. | 卫星在0~t1时间内的加速度大于t1~t2时间内的加速度 | |
| C. | t1~t2时间内卫星处于超重状态,t2~t3时间内卫星处于失重状态 | |
| D. | 卫星在t2~t3时间内的加速度大小大于重力加速度 |
19.在物理现象的发现和物理理论的建立过程中,物理学家总结出许多科学方法.如理想实验、演绎推理、科学假说等.以下观点正确的是( )
| A. | 如果电场线与等势面不垂直,那么电场强度就有一个沿着等势面的分量,在等势面上移动电荷静电力就要做功.这里用的逻辑方法是归纳法 | |
| B. | 安培为解释磁现象提出了“物质微粒内部存在着一种环形电流-分子电流”的观点 | |
| C. | 用比值法来描述加速度这个物理量,其表达式为a=$\frac{F}{m}$ | |
| D. | 牛顿利用“月-地检验”建立了万有引力定律 |
16.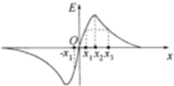 空间有一沿x轴对称分布的电场,电场强度就在x轴上且规定沿x轴正向为正,其电场强度E随x轴变化的图象如图所示,图象过坐标原点O点,下列说法中正确的是( )
空间有一沿x轴对称分布的电场,电场强度就在x轴上且规定沿x轴正向为正,其电场强度E随x轴变化的图象如图所示,图象过坐标原点O点,下列说法中正确的是( )
 空间有一沿x轴对称分布的电场,电场强度就在x轴上且规定沿x轴正向为正,其电场强度E随x轴变化的图象如图所示,图象过坐标原点O点,下列说法中正确的是( )
空间有一沿x轴对称分布的电场,电场强度就在x轴上且规定沿x轴正向为正,其电场强度E随x轴变化的图象如图所示,图象过坐标原点O点,下列说法中正确的是( )| A. | x1和x3两点的电势相等 | |
| B. | 在x轴上场强最大的点有两个,其中一个点是x2 | |
| C. | 坐标原点O点的电势最低 | |
| D. | x1和-x1两点的电势相等 |
17.一列简谐横波在x轴上传播,波源处于x=0m处,在x=3m处的质元P和x=6m处的质元Q的振动图线分别如图甲、乙所示,下列说法正确的( )


| A. | 波长可能是4m | B. | 波的周期一定是12s | ||
| C. | 波的振幅一定是8cm | D. | 波的传播速度一定是1m/s | ||
| E. | 波由P传播到Q历时可能是9s |
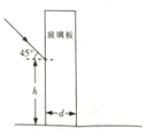 如图所示,银行为了安全在水平柜台上安装了厚度为d的竖直玻璃板,某同学为了粗测其折射率,用一支激光笔在垂直于板面的竖直平面内,让激光以45°的入射角斜向下射向玻璃板,入射点到柜台面的距离为h,他请银行柜员测量了激光透过玻璃板落在柜台面上光点到玻璃板的距离为s.求
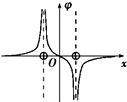
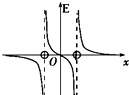
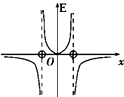
如图所示,银行为了安全在水平柜台上安装了厚度为d的竖直玻璃板,某同学为了粗测其折射率,用一支激光笔在垂直于板面的竖直平面内,让激光以45°的入射角斜向下射向玻璃板,入射点到柜台面的距离为h,他请银行柜员测量了激光透过玻璃板落在柜台面上光点到玻璃板的距离为s.求 如图所示,两个等量正点电荷位于x轴上,相对原点对称分布,下面能够正确描述电势φ和场强E随位置x变化规律的图是( )
如图所示,两个等量正点电荷位于x轴上,相对原点对称分布,下面能够正确描述电势φ和场强E随位置x变化规律的图是( )