题目内容
如图所示，从同一条竖直线上两个不同点P、Q分别向右平抛两个小球，平抛P的初速度分别为v1、v2，结果它们同时落到水平面上的M点处(不考虑空气Q阻力)．下列说法中正确的是( )
| A．一定是P先抛出的，并且v1＝v2 |
| B．一定是P先抛出的，并且v1＜v2 |
| C．一定是Q先抛出的，并且v1＝v2 |
| D．一定是Q先抛出的，并且v1＞v2 |
B
解析试题分析：两小球被抛出后均做平抛运动，根据平抛运动规律可知，在竖直方向上有：h＝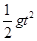
，解得小球运动的时间为：t＝
，由图可知小球P的下落高度h1大于小球Q的下落高度h2，因此两球的运动时间有：t1＞t2，因两球同时落地，所以小球P被先抛出，故选项C、D错误；在水平方向上有：x＝vt，由图可知：x1＝x2，所以v1＜v2，故选项A错误；选项B正确。
考点：本题主要考查了平抛运动规律的应用以及控制变量法的运用问题，属于中档题。
小学夺冠AB卷系列答案两相同高度的斜面，倾角分别为300、600，两小球分别由斜面顶端以相同水平速度v抛出，如图所示，假设两球能落在斜面上，则两球下落高度之比（ ）
| A．1:2 | B．3:1 | C．1:9 | D．9:1 |
“套圈圈”是小孩和大人都喜爱的一种游戏。某小孩和大人直立在界外，在同一竖直线上不同高度分别水平抛出小圆环，并恰好套中前方同一物体。假设小圆环的运动可以视为平抛运动，则
| A．大人抛出的圆环运动时间较短 |
| B．大人应以较小的速度抛出圆环 |
| C．小孩抛出的圆环运动发生的位移较大 |
| D．小孩抛出的圆环单位时间内速度变化量较小 |
如图所示，球网高出桌面H，网到桌边的距离为L。某人在乒乓球训练中，从左侧L/2处，将球沿垂直于网的方向水平击出，球恰好通过网的上沿落到右侧桌边缘。设乒乓球运动为平抛运动。则（ ）
| A．击球点的高度与网高度之比为2：1 |
| B．乒乓球在网左右两侧运动时间之比为2：1 |
| C．乒乓球过网时与落到桌边缘时速率之比为1：2 |
| D．乒乓球在左、右两侧运动速度变化量之比为1： 2 |
水平抛出的小球，t秒末的速度方向与水平方向的夹角为θ1，t+t0秒末速度方向与水平方向的夹角为θ2，忽略空气阻力，则小球初速度的大小为（）
| A．gt0(cosθ1-cosθ2) | B． |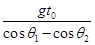
| C．gt0(tanθ1-tanθ2) | D． |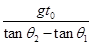
∶1如图所示，AB为半圆环ACB的水平直径，C为环上的最低点．一个小球从A点以不同的初速度v0水平抛出，经一段时间与半圆环相撞，不计空气阻力，下列表述正确的是（ ）
| A．v0越大，运动时间越长。 |
| B．v0 越小，运动时间越长。 |
| C．总可以找到一个v0值，使小球垂直撞击半圆环。 |
| D．无论v0取何值，小球都不可能垂直撞击半圆环。 |
以速度v0水平抛出一小球，如果从抛出到某时刻小球的竖直分位移与水平分位移大小相等，以下判断正确的是
| A．此时小球的竖直分速度大小等于水平分速度大小 |
| B．此时小球速度的方向与位移的方向相同 |
C．小球运动的时间为 |
D．此时小球的速度大小为 |
