题目内容
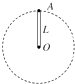
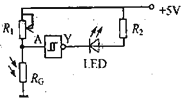
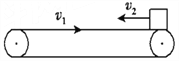
【题目】如图所示为一种加速度仪的示意图。质量为m的振子两端连有劲度系数均为k的轻弹簧,电源的电动势为E , 不计内阻,滑动变阻器的总阻值为R , 有效长度为L , 系统静止时滑动触头位于滑动变阻器正中,这时电压表指针恰好在刻度盘正中。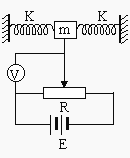
求:
(1)系统的加速度A(以向右为正)和电压表读数U的函数关系式。
(2)将电压表刻度改为加速度刻度后,其刻度是均匀的还是不均匀的?为什么?
(3)若电压表指针指在满刻度的3/4位置,此时系统的加速度大小和方向如何?
【答案】
(1)
当振子向左偏离中间位置x距离时,由牛顿第二定律得 ![]() ①
①
电压表的示数为 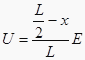 ②
②
由以上两式解得 ![]() ③
③
(2)
均匀,因为加速度A与电压表示数U是一次函数(线性关系)
(3)
当滑动触头滑到最右端时,电压表最大示数 ![]() ,电压表指针指在满刻度的3/4位置时,
,电压表指针指在满刻度的3/4位置时, ![]() 代入③式解得
代入③式解得 ![]() 方向向左
方向向左
【解析】解:(1)当振子向左偏离中间位置x距离时,由牛顿第二定律得 ![]() ①
①
电压表的示数为 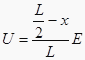 ②
②
由以上两式解得 ![]() ③(2)均匀,因为加速度A与电压表示数U是一次函数(线性关系)。(3)当滑动触头滑到最右端时,电压表最大示数
③(2)均匀,因为加速度A与电压表示数U是一次函数(线性关系)。(3)当滑动触头滑到最右端时,电压表最大示数 ![]() ,电压表指针指在满刻度的3/4位置时,
,电压表指针指在满刻度的3/4位置时, ![]() 代入③式解得
代入③式解得 ![]() 方向向左。
方向向左。
本题通过弹簧振子的简谐振动,将加速度转化为容易测量的电信号,从而实现传感器的功能。

【题目】某同学在研究性学习中记录了一些与地球、月球有关的数据资料如图中表所示,利用这些数据来计算地球表面与月球表面之间的距离s,则下列运算公式中错误的是()
地球半径 | R=6400km |
月球半径 | r=1740km |
地球表面重力加速度 | g0=9.80m/s2 |
月球表面重力加速度 | g′=1.56m/s2 |
月球绕地球转动的线速度 | v=1km/s |
月球绕地球转动周期 | T=27.3天 |
光速 | c=2.998×105 km/s |
用激光器向月球表面发射激光光束,经过约t=2.565s接收到从月球表面反射回来的激光信号 | |
A. s=c![]() B. s=
B. s=![]() ﹣R﹣r
﹣R﹣r
C. s=![]() ﹣R﹣r D. s=
﹣R﹣r D. s=![]() ﹣R﹣r
﹣R﹣r