题目内容
如右图所示,劲度系数为k的轻弹簧,一端固定在一块与水平面夹角为30°的粗糙长木板上,另一端连接一个质量为m的滑块A,滑块与木板的最大静摩擦力为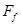 .设滑块与木板的最大静摩擦力与其滑动摩擦力大小相等,且
.设滑块与木板的最大静摩擦力与其滑动摩擦力大小相等,且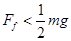 .
.
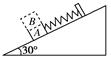
(1)如果保持滑块在木板上静止不动,弹簧的最小形变量为多大?
(2)若在滑块A上再固定一个同样的滑块B,两滑块构成的整体沿木板向下运动,当弹簧的形变量仍为(1)中所求的最小值时,其加速度为多大?
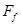 .设滑块与木板的最大静摩擦力与其滑动摩擦力大小相等,且
.设滑块与木板的最大静摩擦力与其滑动摩擦力大小相等,且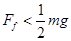 .
.
(1)如果保持滑块在木板上静止不动,弹簧的最小形变量为多大?
(2)若在滑块A上再固定一个同样的滑块B,两滑块构成的整体沿木板向下运动,当弹簧的形变量仍为(1)中所求的最小值时,其加速度为多大?
(1) 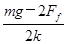 (2)
(2) 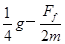
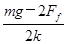 (2)
(2) 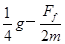
试题分析:(1)由于
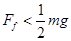 ,因此滑块静止时弹簧一定处于伸长状态,设弹簧最小形变量为
,因此滑块静止时弹簧一定处于伸长状态,设弹簧最小形变量为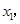 根据共点力平衡条件,
根据共点力平衡条件,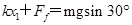
解得
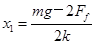 .
.(2)将滑块B固定到A上后,设弹簧伸长量仍为x1时两滑块的加速度为a,根据牛顿第二定律

解得
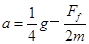 .
.点评:加速度是联系力和运动的桥梁,所以在分析此类型问题时一定要注意受力分析,根据牛顿第二定律求加速度

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
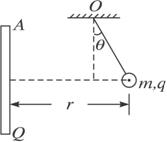
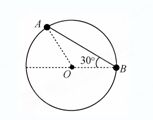


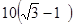 N
N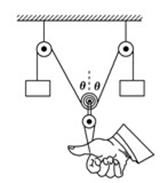
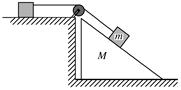
 ,倾角为
,倾角为 的斜面体(斜面光滑且足够长)被固定在水平地面上,斜面顶端与劲度系数为
的斜面体(斜面光滑且足够长)被固定在水平地面上,斜面顶端与劲度系数为 、自然长度为
、自然长度为 的轻质弹簧相连,弹簧的另一端连接着质量为
的轻质弹簧相连,弹簧的另一端连接着质量为 的物块。压缩弹簧使其长度为
的物块。压缩弹簧使其长度为 时将物块由静止开始释放,物块在斜面上做简谐振动,重力加速度为
时将物块由静止开始释放,物块在斜面上做简谐振动,重力加速度为 。
。
