题目内容
【题目】如图所示，以A、B为端点的半圆形光滑轨道固定于竖直平面内，一粗糙水平面BC与半圆形轨道相切于B点。质量为2m的物块1被轻放在水平匀速运动的传送带上G点，运动到A时刚好与传送带速度相同，然后经A沿半圆轨道滑下，再经B滑上BC，在C处与质量为m的物块2相碰（相碰没有能量损失）。倾斜角为37°、高为3R斜面与BC和水平地面FE相接，已知CEF表面有一层很厚的细砂，以阻止物块运动。物块均可视为质点，半圆半径为R，BC长LBC =2R。G距A为S=5R，物块与传送带、物块与BC间的动摩擦系数均为μ=0. 5，重力加速度取g。（sin37°=0.6，cos37°=0.8）
（1）求物块滑到B点的速度大小。
（2）求物块1与物块2碰撞后，在空中运动的时间。
【答案】（1）
（2）
【解析】（1）由动能定理可得
①，所以
②
（2）物块由B到C： 
③，解得
④
两物块碰撞： 
， 
解得
，
判断：求物块平抛到EF的最小速度
，⑤
⑥
由⑤⑥得
因
，物块1落在斜面上
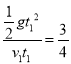故物块1在空中运动的时间
因
故物块2被直接平抛到EF上。
故由⑥得物块2从C点运动到地面所需时间
练习册系列答案
相关题目
