题目内容
如图所示,长l的细绳一端系质量m的小球,另一端固定于O点,细绳所能承受拉力的最大值是7mg.现将小球拉至水平并由静止释放,又知图中O′点有一小钉,为使小球可绕O′点做竖直面内的圆周运动.试求OO′的长度d与θ角应满足的关系(设绳与小钉O′相互作用中无能量损失).
解析:本题考查圆周运动、动能定理、机械能守恒的应用,在临界状态的受力和特点是本题的难点,
设小球能绕O′点完成圆周运动,如图所示.其最高点为D,最低点为C.对于D点,依向心力公式有
(1)(2分)
其中vD为D点速度,vD可由机械能守恒定律求知,取O点为重力势能的零势能位置,则
(2)(2分)
将(1)式与(2)式联立,解之可得(1分)
另依题意细绳上能承受的最大拉力不能超过7mg,由于在最低点C,绳所受拉力最大,故应以C点为研究对象,并有
(3) (1分) 其中vC是C点速度,
可由机械能守恒定律求知(4) (2分)
将(3)式与(4)式联立,解之可得(1分)
(1分)

练习册系列答案
相关题目
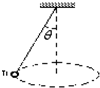 如图所示,长L的细绳,一端固定于o点,另一端系一质量为m的小球.小球在水平面内做匀速圆周运动,运动时细绳和竖直方向成θ角.以下说法正确的是( )
如图所示,长L的细绳,一端固定于o点,另一端系一质量为m的小球.小球在水平面内做匀速圆周运动,运动时细绳和竖直方向成θ角.以下说法正确的是( )| A、小球受到重力,绳的拉力和向心力作用 | B、小球受到重力和绳的拉力作用 | C、绳的拉力就是向心力 | D、小球受到的向心力等于mgtanθ |


