题目内容
9.宇宙中有一星球的质量约为地球质量的9倍,半径约为地球半径的一半.若从地球上h(此高度比较小)处水平抛出一物体,水平射程是30m,设地球第一宇宙速度约为8km/s,试求:(1)则在该星球上,从同样高度以同样的初速度水平抛出同一物体,射程是多少?
(2)至少以多大的速度抛出,物体才不会落回该星球的表面?(提示:此时恰能在地球表面附近绕地球做匀速圆周运动).
分析 (1)根据万有引力等于重力得出星球表面和地球表面重力加速度的关系,结合平抛运动的规律求出射程的大小.
(2)根据重力提供向心力得出第一宇宙速度的表达式,从而结合重力加速度之比求出在星球上的第一宇宙速度,即不会落回星球表面的最小速度.
解答 解:(1)根据$G\frac{Mm}{{R}^{2}}=mg$得,g=$\frac{GM}{{R}^{2}}$,
因为星球的质量是地球质量的9倍,半径为地球半径的一半,则重力加速度36倍.
根据h=$\frac{1}{2}g{t}^{2}$,x=vt知,水平射程x=$v\sqrt{\frac{2h}{g}}$,
因为重力加速度之比为36:1,则水平射程之比为1:6,
可知在该星球上,从同样高度以同样的初速度水平抛出同一物体,射程x′=$30×\frac{1}{6}m=5m$.
(2)根据mg=m$\frac{{v}^{2}}{R}$得,第一宇宙速度v=$\sqrt{gR}$,
因为重力加速度之比为36:1,半径之比为1:2,则第一宇宙速度之比为$\sqrt{18}:1$,
解得最小速度v′=8×$\sqrt{18}$km/s=24$\sqrt{2}$km/s.
答:(1)在该星球上,从同样高度以同样的初速度水平抛出同一物体,射程是5m;
(2)至少以$24\sqrt{2}$km/s的速度抛出,物体才不会落回该星球的表面.
点评 本题考查了平抛运动规律与万有引力定律理论的综合运用,通过万有引力等于重力求出重力加速度之比是解决本题的关键.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
7. 甲、乙两车在同一水平路面上的两平行车道做直线运动,某时刻乙车在前、甲车在后,相距6m,从此刻开始计时,两车运动的v-t图象如图所示,在0一8s内,下列说法正确的是( )
甲、乙两车在同一水平路面上的两平行车道做直线运动,某时刻乙车在前、甲车在后,相距6m,从此刻开始计时,两车运动的v-t图象如图所示,在0一8s内,下列说法正确的是( )
 甲、乙两车在同一水平路面上的两平行车道做直线运动,某时刻乙车在前、甲车在后,相距6m,从此刻开始计时,两车运动的v-t图象如图所示,在0一8s内,下列说法正确的是( )
甲、乙两车在同一水平路面上的两平行车道做直线运动,某时刻乙车在前、甲车在后,相距6m,从此刻开始计时,两车运动的v-t图象如图所示,在0一8s内,下列说法正确的是( )| A. | t=4s时两车相距2m | B. | t=4s时两车相遇 | ||
| C. | t=8s时两车相遇 | D. | 开始时两车相距最远 |
14. 如图所示,先后以速度v1和v2匀速把一矩形线圈拉出有界匀强磁场区域,v1=2v2.在先后两种情况下( )
如图所示,先后以速度v1和v2匀速把一矩形线圈拉出有界匀强磁场区域,v1=2v2.在先后两种情况下( )
 如图所示,先后以速度v1和v2匀速把一矩形线圈拉出有界匀强磁场区域,v1=2v2.在先后两种情况下( )
如图所示,先后以速度v1和v2匀速把一矩形线圈拉出有界匀强磁场区域,v1=2v2.在先后两种情况下( )| A. | 线圈中的感应电流之比为I1:I2=1:2 | |
| B. | 线圈中的感应电流之比为I1:I2=2:1 | |
| C. | 通过线圈某截面的电荷量之比q1:q2=1:2 | |
| D. | 通过线圈某截面的电荷量之比q1:q2=2:1 |
18.媒体2015年1月9日消息:据物理学家组织网站报道,船底座是由两颗大质量恒星组成的双星系统,这两颗恒星以5.5年的周期围绕共同的质心运行.若把它们的运动视为匀速圆周运动,则( )
| A. | 它们做圆周运动的角速度与它们的质量成反比 | |
| B. | 它们做圆周运动的周期与它们的质量成反比 | |
| C. | 它们做圆周运动的半径与它们的质量成反比 | |
| D. | 它们所受的向心力与它们的质量成反比 |
 如图所示,一根轻质弹簧的下端固定在水平桌面上,上端固定一个质量为m=1kg的物体A,A静止时弹簧的压缩量x=16cm.在A上再放一个质量与A相等的物体B,待A、B静止后,再在B上施加一个竖直向下的力F缓慢地压弹簧,该力使弹簧又缩短了3x,这时弹簧的弹性势能为Ep=20J(g取10m/s2)求:
如图所示,一根轻质弹簧的下端固定在水平桌面上,上端固定一个质量为m=1kg的物体A,A静止时弹簧的压缩量x=16cm.在A上再放一个质量与A相等的物体B,待A、B静止后,再在B上施加一个竖直向下的力F缓慢地压弹簧,该力使弹簧又缩短了3x,这时弹簧的弹性势能为Ep=20J(g取10m/s2)求:

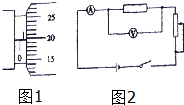 在“测定金属丝电阻率”的实验中,需要测出其长度L,直径d和电阻R.
在“测定金属丝电阻率”的实验中,需要测出其长度L,直径d和电阻R.