��Ŀ����
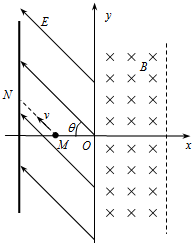
18����ͼ��ʾ������ֱƽ���ڽ���Oxyֱ������ϵ����x=-$\sqrt{2}$d���д�ֱ��x���㹻��ĵ��Ծ�Ե���壬y�����͵���֮�����һ��ǿ�糡���糡��x�Ḻ����нǦ�=45�㣬y���Ҳ���һ���н���ǿ�ų����ų�����ֱ��ֽ������Ÿ�Ӧǿ�ȴ�СΪB����M��-$\frac{\sqrt{2}}{2}$d��0������һ������Ϊm�������Ϊ-q�����ӣ���ijһ���ٶ��س�ǿ�����˶���������Ե����N��ʱ��������y�᷽����ٶȲ��䣬x�᷽���ٶȴ�С���䡢������һ��ʱ�����$\sqrt{2}$v���ٶȴ�ֱ��y�����ų���ǡ�ò��Ӵų��ұ߽�ɳ������ӵ��������ƣ���1����ų��Ŀ���L��
��2������ǿ�糡�ij�ǿ��СE��
��3������һ��ͬ�����������ٶ�v��M���س�ǿ�����˶�����ʱ��t��һ�δӴų��߽���P���������ʱ��t��
���� ��1���������������ṩ���������ٽ��������ɼ���֪ʶ���Բ���˶��İ뾶�����������������L�Ĵ�С��
��2���ɶ��ܶ�����������糡ǿ�ȵĴ�С��
��3���ȸ����˶�ѧ�Ĺ�ʽ��������ڵ糡���˶���ʱ�䣬Ȼ���ɼ��ι�ʽt=$\frac{��}{2��}$T���Բ���˶���ʱ�䣬��������˶������ε���ʱ�䣮
��� �⣺��1���������������ṩ�������У�$\sqrt{2}qvB=\frac{m��\sqrt{2}v��^{2}}{R}$
��ã�$R=\frac{\sqrt{2}mv}{qB}$
���Ӹպò��뿪�ų�������Ϊ��L=R������$L=\frac{\sqrt{2}mv}{qB}$
��2����ͼ�������Ӵ�A�����ų��������N�㵽A����˶��ֱ����ŵ糡�ߺʹ�ֱ�糡�߷���ֽ⣬������������������ͨ���ľ���ֱ�Ϊh��l����A�����������������ٶȴ�С��Ϊv��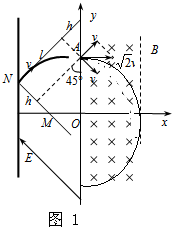
�ص糡�߷����У�$h=\frac{1}{2}��\frac{qE}{m}•{t}^{2}=\frac{vt}{2}$
��ֱ�ڵ糡�߷����У�l=vt
�ɼ��ι�ϵ�У�l+h=2d
���ϸ�ʽ�����ã�$E=\frac{3m{v}^{2}}{4qd}$
��3�����Ӵ�M���ص糡�߷�����ǰ�˶��ľ���Ϊs
��v2=2as �ã�$s=\frac{{v}^{2}}{2•\frac{qE}{m}}=\frac{2}{3}d��d$
˵�����Ӳ��ܴ�Ե���Ͼ�Ҫ���أ��˶�������ͼ
��P�����ų�ʱ������Ϊv�䣬��v��2-v2=2ad
��ã�$v��=\frac{\sqrt{10}}{2}v$
�����ڵ糡�������˶���ʱ��Ϊ��${t}_{1}=\frac{v+v��}{a}=\frac{��4+2\sqrt{10}��d}{3v}$
�����ڴų���Բ���˶��İ뾶��$R��=\frac{mv��}{qB}=\frac{\sqrt{10}mv}{2qB}$
��ΪR�䣨1-cos45�㣩��L���������Ӳ���Ӵų��ұ߽������
�����ڴų�����Բ���˶������ڣ�$T=\frac{2��m}{qB}$
�ڴų����˶���ʱ��Ϊ��${t}_{2}=\frac{T}{4}=\frac{��m}{2qB}$
���Ӵ�M���������һ�δӴų��г�����������ʱ��Ϊ
t=t1+t2=$\frac{��4+2\sqrt{10}��d}{3v}+\frac{��m}{2qB}$
�𣺣�1���ų��Ŀ���$\frac{\sqrt{2}mv}{qB}$��
��2����ǿ�糡�ij�ǿ��С��$\frac{3m{v}^{2}}{4qd}$��
��3��ʱ����$\frac{��4+2\sqrt{10}��d}{3v}+\frac{��m}{2qB}$��
���� ���⿼����������ڴų��к͵糡�е��˶������Ĺؼ�����ȷ���ӵ��˶����ɣ������˶��켣��Ȼ����ͼ���еļ��ι�ϵ��ȷ���켣��Բ����뾶��Ȼ����ţ�ٵڶ����ɼ�����⣮

 ����Һʱ��ҩҺ��ʱ�������������⣬Ϊ�˼�ʱ���֣�ij�������һ���Զ�����װ�ã���·��ͼ��ʾ����ֵ����R��̽����S��������ֲ��䣮M��������ڴ��Ĵ����������Ӵ���ҩҺʱ�����RM�ᷢ�����Ա仯������S���˵�ѹU����װ�÷�����������ʱ��������
����Һʱ��ҩҺ��ʱ�������������⣬Ϊ�˼�ʱ���֣�ij�������һ���Զ�����װ�ã���·��ͼ��ʾ����ֵ����R��̽����S��������ֲ��䣮M��������ڴ��Ĵ����������Ӵ���ҩҺʱ�����RM�ᷢ�����Ա仯������S���˵�ѹU����װ�÷�����������ʱ��������| A�� | RM�����RԽ��̽����SԽ���� | B�� | RM�����RԽС��̽����SԽ���� | ||
| C�� | RM��С����RԽ��̽����SԽ���� | D�� | RM��С����RԽС��̽����SԽ���� |
| A�� | M�����������������ȵ�ʱ����ת���ĽǶȽϴ� | |
| B�� | M�Ļ�е�ܴ���N�Ļ�е�� | |
| C�� | M��N���ٶȾ����ڵ�һ�����ٶ� | |
| D�� | M����ͬ��ʱ���ھ�����·�̽϶� |
| A�� | ��г�˶�������������� | |
| B�� | �ڵ�����������г�˶��Ļظ�������ʽF=-kx�У�FΪ�������ܵ��ĺ�������kΪ���ɵľ���ϵ�� | |
| C�� | �ڲ����������ϣ�ij���ʵ�����ٶȾ��Dz��Ĵ����ٶ� | |
| D�� | ��˫�����ʵ���У�ͬ�����������Ϲ���ʵ��Ⱥ����ʵ��õ������Ƹ��� |
| A�� | ������������������ʶ����и������� | |
| B�� | ������Һ���еĻ��ۿ����������˶������˶� | |
| C�� | ��ͬ�¶��£�����ӵ�ƽ������һ�������������ӵ�ƽ������ | |
| D�� | ���ŷ��Ӽ���������Ӽ���������С����������Ҳ��С |
| A�� | �����϶��µ������� | |
| B�� | �����¶��ϵ������� | |
| C�� | ���������������������϶��£������¶��� | |
| D�� | ���������������������¶��ϣ������϶��� |
| A�� | $\frac{{{E_{k1}}}}{{{E_{k2}}}}$ | B�� | $\frac{{{E_{k2}}}}{{{E_{k1}}}}$ | C�� | $\sqrt{{{��{\frac{{{E_{k1}}}}{{{E_{k2}}}}}��}^3}}$ | D�� | $\sqrt{{{��{\frac{{{E_{k2}}}}{{{E_{k1}}}}}��}^3}}$ |
| A�� | ��������ײ������ͬһ����� | |
| B�� | ��������ײ���ǵ����ڡ����ļ��ٶȴ�Сһ����� | |
| C�� | ����ײ���ǵ������ٶȾ����ڹ��ʿռ�վ���ٶ� | |
| D�� | ����ײ���ǵ��������ھ����ڹ��ʿռ�վ���������� |
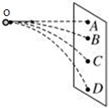 ��ͼ��ʾ��ijͬѧ��С���O���Բ�ͬ�ij�����ˮƽ�׳����ֱ���ڵ����ϵ�B��C��D������֪A��O��ͬһ�߶ȣ���AB��BC��CD=1��3��5����С��ij����ֱܷ�ΪEk1��Ek2��Ek3��������
��ͼ��ʾ��ijͬѧ��С���O���Բ�ͬ�ij�����ˮƽ�׳����ֱ���ڵ����ϵ�B��C��D������֪A��O��ͬһ�߶ȣ���AB��BC��CD=1��3��5����С��ij����ֱܷ�ΪEk1��Ek2��Ek3��������| A�� | Ek1��Ek2��Ek3=9��4��1 | B�� | Ek1��Ek2��Ek3=25��9��1 | ||
| C�� | Ek1��Ek2��Ek3=81��16��1 | D�� | Ek1��Ek2��Ek3=36��9��4 |