题目内容
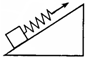 一个木块放在斜面上,用沿斜面方向的轻弹簧拉着处于静止.要使木块静止在斜面上,弹簧的最小伸长为△L1,最大伸长为△L2,已知弹簧的倔强系数为k.木块在斜面上受到的最大静摩擦力是多少?
一个木块放在斜面上,用沿斜面方向的轻弹簧拉着处于静止.要使木块静止在斜面上,弹簧的最小伸长为△L1,最大伸长为△L2,已知弹簧的倔强系数为k.木块在斜面上受到的最大静摩擦力是多少?分析:若拉力较小,则木块有向下运动趋势时受沿斜面上的最大静摩擦力,此时弹簧有最小伸长;若拉力较大,则木块有向上运动的趋势时沿斜面向下的最大静摩擦力,此时弹簧有最大伸长.然后根据平衡条件列方程求解.
解答:解:若拉力较小,则木块有向下运动趋势时受沿斜面上的最大静摩擦力,根据平衡条件:
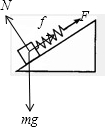
f+k△L1=mgsinθ ①
若拉力较大,则木块有向上运动的趋势时,木块受到沿斜面向下的最大静摩擦力,
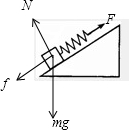
f+mgsinθ=k△l2②
联立①②得:f=
.
答:木块在斜面上受到的最大静摩擦力是
.

f+k△L1=mgsinθ ①
若拉力较大,则木块有向上运动的趋势时,木块受到沿斜面向下的最大静摩擦力,

f+mgsinθ=k△l2②
联立①②得:f=
| k(△L2-△L1) |
| 2 |
答:木块在斜面上受到的最大静摩擦力是
| k(△L2-△L1) |
| 2 |
点评:本题解答的关键是分析何时弹簧伸长量最大何时弹簧伸长量最小,再由平衡条件分析求解静摩擦力.

练习册系列答案
相关题目