题目内容
20.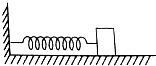 如图所示,一个弹簧振子,物块质量为m,它与水平桌面间的动摩擦因数为μ.起初用手按住物块,弹簧的伸长量为x,然后放手,当弹簧的长度回到原长时,物块的速度为v0,则此过程中弹力所做的功为( )
如图所示,一个弹簧振子,物块质量为m,它与水平桌面间的动摩擦因数为μ.起初用手按住物块,弹簧的伸长量为x,然后放手,当弹簧的长度回到原长时,物块的速度为v0,则此过程中弹力所做的功为( )| A. | $\frac{1}{2}$mv02+μmgx | B. | $\frac{1}{2}$mv02-μmgx | C. | $\frac{1}{2}$mv02 | D. | μmgx-$\frac{1}{2}$mv02 |
分析 对物体而言,除弹簧弹力外,还要克服滑动摩擦力做功,根据动能定理列式即可求解出弹簧弹力做的功.
解答 解:对物块,由动能定理得:W-μmgx=$\frac{1}{2}$mv02-0,
解得,弹簧弹力做功:W=μmgx+$\frac{1}{2}$mv02,故A正确;
故选:A.
点评 本题考查了动能定理的应用,分析清楚物体的运动过程,应用动能定理即可正确解题,本题是一道基础题.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
15. 如图所示,在场强大小为 E 的匀强电场中,有一个边长为L的正方形区域,正方形的一条边与电场方向平行.质量为m、电荷量绝对值为q的电子从某一条边的中点,以初速度v0射入该区域.初速度的方向垂直指向对边,但电子没有从对边飞出.下列说法正确的是( )
如图所示,在场强大小为 E 的匀强电场中,有一个边长为L的正方形区域,正方形的一条边与电场方向平行.质量为m、电荷量绝对值为q的电子从某一条边的中点,以初速度v0射入该区域.初速度的方向垂直指向对边,但电子没有从对边飞出.下列说法正确的是( )
 如图所示,在场强大小为 E 的匀强电场中,有一个边长为L的正方形区域,正方形的一条边与电场方向平行.质量为m、电荷量绝对值为q的电子从某一条边的中点,以初速度v0射入该区域.初速度的方向垂直指向对边,但电子没有从对边飞出.下列说法正确的是( )
如图所示,在场强大小为 E 的匀强电场中,有一个边长为L的正方形区域,正方形的一条边与电场方向平行.质量为m、电荷量绝对值为q的电子从某一条边的中点,以初速度v0射入该区域.初速度的方向垂直指向对边,但电子没有从对边飞出.下列说法正确的是( )| A. | 电场方向可能与初速度方向相反 | |
| B. | 电场方向可能与初速度方向垂直 | |
| C. | 电子离开该区域时,动能可能为$\frac{1}{2}$mv02 | |
| D. | 电子离开该区域时,动能可能为$\frac{1}{2}$mv02+$\frac{1}{2}$qEL |
2.如图1所示,单匝矩形线框相邻两边分别长为L和2L,从中线OO′处对折,且保持折角θ=90°不变.如图2所示,使线框在水平向右的匀强磁场中以角速度ω绕竖直方向的OO′轴匀速转动.匀强磁场的磁感应强度大小为B,线框电阻为R,从图2所示位置(线框的OO′CD部分与中性面重合)开始计时,取A→B→C→D→A为线框中感应电流的正方向,下列说法正确的是( )

| A. | 线框中感应电流i随时间t的变化关系是i=$\frac{{\sqrt{2}B{L^2}ω}}{R}$cos(ωt+$\frac{π}{4}$) | |
| B. | 线框中感应电流i随时间t的变化关系是i=$\frac{{B{L^2}ω}}{R}$•cosωt | |
| C. | 在t=0时刻,线框中的感应电流最大 | |
| D. | 从0~$\frac{π}{2ω}$时间内,感应电流方向改变1次 |
9. 如图所示,半圆形轨道凹槽静止放置在水平地面上,A点位于半圆形凹槽左边缘,B点位于凹槽上某一点,轨道半径为R,在AB间斜靠一光滑且足够长的木板,在A点有a、b两球(视为质点),a球由静止释放沿斜面下滑到B点,同时b球以某速度v0水平抛出,正好打在B点,则下列说法正确的是( )
如图所示,半圆形轨道凹槽静止放置在水平地面上,A点位于半圆形凹槽左边缘,B点位于凹槽上某一点,轨道半径为R,在AB间斜靠一光滑且足够长的木板,在A点有a、b两球(视为质点),a球由静止释放沿斜面下滑到B点,同时b球以某速度v0水平抛出,正好打在B点,则下列说法正确的是( )
 如图所示,半圆形轨道凹槽静止放置在水平地面上,A点位于半圆形凹槽左边缘,B点位于凹槽上某一点,轨道半径为R,在AB间斜靠一光滑且足够长的木板,在A点有a、b两球(视为质点),a球由静止释放沿斜面下滑到B点,同时b球以某速度v0水平抛出,正好打在B点,则下列说法正确的是( )
如图所示,半圆形轨道凹槽静止放置在水平地面上,A点位于半圆形凹槽左边缘,B点位于凹槽上某一点,轨道半径为R,在AB间斜靠一光滑且足够长的木板,在A点有a、b两球(视为质点),a球由静止释放沿斜面下滑到B点,同时b球以某速度v0水平抛出,正好打在B点,则下列说法正确的是( )| A. | a、b两球有可能同时到达B点 | |
| B. | b球打在B点的速度方向可能垂直于该点的切线方向 | |
| C. | 若a球到达B点的时间是b球的两倍,则木板与水平方向的夹角是60° | |
| D. | 撤去木板,如果v0=$\sqrt{gR}$时,则可判断b球落点位于凹槽最低点的右侧 |
7. 有一种静电除尘的方式,如图所示,空气中的尘埃进入电离区后带上负电,然后沿平行轴线飞入金属圆筒收集区.在圆筒轴线处放有一条直线,在导线与筒壁间加上电压U,形成沿半径方向的辐向电场,假设每个尘埃的质量和带电量均相同,飞入收集区的速度相同,不计尘埃的重力,不考虑尘埃间的相互作用,则( )
有一种静电除尘的方式,如图所示,空气中的尘埃进入电离区后带上负电,然后沿平行轴线飞入金属圆筒收集区.在圆筒轴线处放有一条直线,在导线与筒壁间加上电压U,形成沿半径方向的辐向电场,假设每个尘埃的质量和带电量均相同,飞入收集区的速度相同,不计尘埃的重力,不考虑尘埃间的相互作用,则( )
 有一种静电除尘的方式,如图所示,空气中的尘埃进入电离区后带上负电,然后沿平行轴线飞入金属圆筒收集区.在圆筒轴线处放有一条直线,在导线与筒壁间加上电压U,形成沿半径方向的辐向电场,假设每个尘埃的质量和带电量均相同,飞入收集区的速度相同,不计尘埃的重力,不考虑尘埃间的相互作用,则( )
有一种静电除尘的方式,如图所示,空气中的尘埃进入电离区后带上负电,然后沿平行轴线飞入金属圆筒收集区.在圆筒轴线处放有一条直线,在导线与筒壁间加上电压U,形成沿半径方向的辐向电场,假设每个尘埃的质量和带电量均相同,飞入收集区的速度相同,不计尘埃的重力,不考虑尘埃间的相互作用,则( )| A. | 大量尘埃将聚集在导线上 | |
| B. | 尘埃在圆筒内都做类似平抛的运动 | |
| C. | 被收集尘埃的电势能减少量都相等 | |
| D. | 飞入时与圆筒轴线距离相同的尘埃到达筒壁所用的时间相同 |
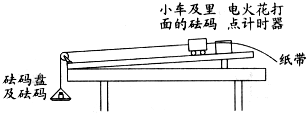 一小组的同学用如图所示的装置探究小车动能变化与合力功的关系,他们将砝码和砝码盘的重力作为小车受到的合力.
一小组的同学用如图所示的装置探究小车动能变化与合力功的关系,他们将砝码和砝码盘的重力作为小车受到的合力. 如图,质量为M=1kg的物块静止在桌面边缘,桌面离水平地面的高度为h=1.8m.一质量为m=20g的子弹以水平速度v0=20m/s射入物块,在很短的时间内以水平速度v1=10m/s穿出木块.重力加速度g取10m/s2,求:
如图,质量为M=1kg的物块静止在桌面边缘,桌面离水平地面的高度为h=1.8m.一质量为m=20g的子弹以水平速度v0=20m/s射入物块,在很短的时间内以水平速度v1=10m/s穿出木块.重力加速度g取10m/s2,求: