题目内容
质量为m的小球，用长为l的线悬挂在O点，在O点正下方l/2处有一光滑的钉子O/，把小球拉到与O/在同一水平面的位置，摆线被钉子拦住，如图所示，将小球从静止释放，当球第一次通过最低点P时 
| A．小球速率突然减小 | B．小球向心力突然增大 |
| C．小球的向心加速度突然减小 | D．摆线上的张力突然增大 |
C
解析试题分析：让小球从静止释放，当小球第一次经过最低点时，小球受到的拉力和重力都与速度垂直，其线速度不会瞬时变化，圆周运动的圆心由O变到O/，运动半径变大，根据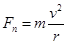
知，向心力突然变小，由
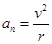知，小球的向心加速度突然减小，由
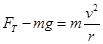知，摆线上张力突然变小，故A、B、D错误，C正确。
考点：本题考查圆周运动相关知识和牛顿第二定律，意在考查考生综合分析问题的能力。
如图所示，某同学用硬塑料管和一个质量为m的铁质螺丝帽研究匀速圆周运动，将螺丝帽套在塑料管上，手握塑料管使其保持竖直并在水平方向做半径为r的匀速圆周运动，则只要运动角速度合适，螺丝帽恰好不下滑，假设螺丝帽与塑料管间的动摩擦因数为μ，认为最大静摩擦力近似等于滑动摩擦力．则在该同学手转塑料管使螺丝帽恰好不下滑时，下述分析正确的是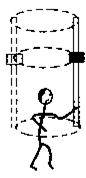
| A．螺丝帽受的重力与最大静摩擦力平衡 |
| B．水平向外，背离圆心 |
C．此时手转动塑料管的角速度ω= |
| D．若杆的转动加快，螺丝帽有可能相对杆发生运动 |
如图所示，一圆环以直径AB为轴做匀速转动，P、Q、R是环上的三点，则下列说法正确的是（ ）
| A．向心加速度的大小aP＝aQ＝aR |
| B．任意时刻P、Q、R三点向心加速度的方向不同 |
| C．线速度vP>vQ>vR |
| D．任意时刻P、Q、R三点的线速度方向均不同 |
长度为1m的轻杆OA，A端有一质量为2kg的小球，以O点为圆心，在竖直平面内做圆周运动，如图所示，小球通过最高点时的速度为3m/s，取g=10m/s2，则此时小球将（ ）
| A．受到18N的拉力 | B．受到38N的支持力 | C．受到2N的拉力 | D．受到2N的支持力 |
一质点沿螺旋线自外向内运动，如图所示。已知其走过的弧长s与时间t的一次方成正比。则关于该质点的运动下列说法正确的是（ ）
| A．小球运动的线速度越来越大 |
| B．小球运动的加速度越来越大 |
| C．小球运动的角速度越来越大 |
| D．小球所受的合外力不变 |
如图所示，轻杆长为L.一端固定在水平轴上的O点，另一端系一个小球(可视为质点)．小球以O为圆心在竖直平面内做圆周运动，且能通过最高点，g为重力加速度．下列说法正确的是 
A．小球通过最高点时速度不可能小于 |
| B．小球通过最高点时所受轻杆的作用力可能为零 |
| C．小球通过最高点时所受轻杆的作用力随小球速度的增大而增大 |
| D．小球通过最高点时所受轻杆的作用力随小球速度的增大而减小 |
如图为一陀螺，a、b、c为在陀螺上选取的三个质点，它们的质量之比为1∶2∶3，它们到转轴的距离之比为3∶2∶1，当陀螺以角速度ω高速旋转时( )
| A．a、b、c的线速度之比为1∶2∶3 |
| B．a、b、c的周期之比为3∶2∶1 |
| C．a、b、c的向心加速度之比为3∶2∶1 |
| D．a、b、c的向心力之比为1∶1∶1 |