题目内容
11.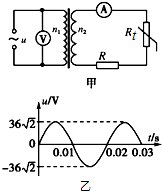 如图甲为理想变压器的示意图,其原、副线圈的匝数比为4:1,电压表和电流表均为理想电表,Rt为阻值随温度升高而变大的热敏电阻,R为定值电阻.若发电机向原线圈输入如图乙所示的正弦交流电,则下列说法正确的是( )
如图甲为理想变压器的示意图,其原、副线圈的匝数比为4:1,电压表和电流表均为理想电表,Rt为阻值随温度升高而变大的热敏电阻,R为定值电阻.若发电机向原线圈输入如图乙所示的正弦交流电,则下列说法正确的是( )| A. | 变压器副线圈输出电压的有效值为9V | |
| B. | t=0.015s时,发电机的线圈平面与磁场方向垂直 | |
| C. | Rt温度升高时,电流表的示数变小,电压表的读数也变小 | |
| D. | 温度升高时,R的电功率增大 |
分析 由图乙可知交流电压最大值Um=36$\sqrt{2}$V,周期T=0.02s,可由周期求出角速度的值,则可得交流电压u的表达式U=36$\sqrt{2}$sin100πtV、由变压器原理可得变压器原、副线圈中的电流之比,Rt处温度升高时,阻值减小,根据负载电阻的变化,可知电流.
解答 解:A、由图乙可知交流电压最大值Um=36$\sqrt{2}$V,${U}_{1}=\frac{36\sqrt{2}}{\sqrt{2}}V=36V$,根据$\frac{{U}_{1}}{{U}_{2}}=\frac{{n}_{1}}{{n}_{2}}$得:${U}_{2}=\frac{{n}_{2}}{{n}_{1}}{U}_{1}=\frac{1}{4}×36V=9V$,故A正确;
B、周期T=0.02s,可由周期求出角速度的值为ω=$\frac{2π}{0.02}$=100πrad/s,则可得交流电压u的表达式 U=36$\sqrt{2}$sin100πtV,当t=0.015s时,$u=36\sqrt{2}sin100π×0.015V=-36\sqrt{2}V$,此时电动势最大,发电机的线圈平面与磁场方向平行,故B错误;
C、t处温度升高时,阻值增大,电流表的示数减小,因为输入电压不变,所以电压表示数不变,故C错误;
D、t处温度升高时,阻值增大,电流表的示数减小,R为定值电阻,根据P=I2R可知电功率减小,故D错误;
故选:A.
点评 根据图象准确找出已知量,是对学生认图的基本要求,准确掌握理想变压器的特点及电压、电流比与匝数比的关系,是解决本题的关键.

练习册系列答案
相关题目
1. 扫地机器人是智能家用电器的一种,它利用自身携带的小型吸尘部件进行吸尘清扫,如图为科沃斯520扫地机器人,已知其工作额定电压15V,额定功率30W,充电额定电压24V,额定电流0.5A,充电时间约240分钟,电池容量2000mAh,则下列说法正确的是( )
扫地机器人是智能家用电器的一种,它利用自身携带的小型吸尘部件进行吸尘清扫,如图为科沃斯520扫地机器人,已知其工作额定电压15V,额定功率30W,充电额定电压24V,额定电流0.5A,充电时间约240分钟,电池容量2000mAh,则下列说法正确的是( )
 扫地机器人是智能家用电器的一种,它利用自身携带的小型吸尘部件进行吸尘清扫,如图为科沃斯520扫地机器人,已知其工作额定电压15V,额定功率30W,充电额定电压24V,额定电流0.5A,充电时间约240分钟,电池容量2000mAh,则下列说法正确的是( )
扫地机器人是智能家用电器的一种,它利用自身携带的小型吸尘部件进行吸尘清扫,如图为科沃斯520扫地机器人,已知其工作额定电压15V,额定功率30W,充电额定电压24V,额定电流0.5A,充电时间约240分钟,电池容量2000mAh,则下列说法正确的是( )| A. | 电池容量是指电池储存电能的大小 | |
| B. | 机器人正常工作的电压为24V | |
| C. | 机器人正常工作时的电流为2A | |
| D. | 机器人充满电后一次工作时间最多约为1小时 |
2.某核反应方程如下:
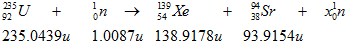
反应方程下方的数据是中子及相关原子核的静止质量.则( )
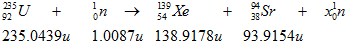
反应方程下方的数据是中子及相关原子核的静止质量.则( )
| A. | x=3 | |
| B. | 反应过程中亏损的质量为0.1933u | |
| C. | 该核反应为核聚变 | |
| D. | 铀核的半衰期会受环境温度的影响而改变 |
19. 如图所示,匀强磁场的边界为直角三角形abc,今有质量为m、带电量为q的一束微观粒子以不同的速度v沿ca方向从c点射入磁场做匀速圆周运动,不计粒子的重力,下列说法中正确的是( )
如图所示,匀强磁场的边界为直角三角形abc,今有质量为m、带电量为q的一束微观粒子以不同的速度v沿ca方向从c点射入磁场做匀速圆周运动,不计粒子的重力,下列说法中正确的是( )
 如图所示,匀强磁场的边界为直角三角形abc,今有质量为m、带电量为q的一束微观粒子以不同的速度v沿ca方向从c点射入磁场做匀速圆周运动,不计粒子的重力,下列说法中正确的是( )
如图所示,匀强磁场的边界为直角三角形abc,今有质量为m、带电量为q的一束微观粒子以不同的速度v沿ca方向从c点射入磁场做匀速圆周运动,不计粒子的重力,下列说法中正确的是( )| A. | 粒子带负电 | |
| B. | 只要速度合适,粒子可以到达b点 | |
| C. | 从bc边射出的所有粒子在磁场中运动的时间相等 | |
| D. | 从ab边射出的粒子一定比从bc边射出的粒子速度大 |
6. 2012年5月6日,天空出现“超级大月亮”,月亮的亮度和视觉直径都大于平常.究其原因,月球的绕地运动轨道实际上是一个偏心率很小的椭圆,当天月球刚好运动到近地点.结合所学知识判断,下列与月球椭圆轨道运动模型有关的说法中正确的是( )
2012年5月6日,天空出现“超级大月亮”,月亮的亮度和视觉直径都大于平常.究其原因,月球的绕地运动轨道实际上是一个偏心率很小的椭圆,当天月球刚好运动到近地点.结合所学知识判断,下列与月球椭圆轨道运动模型有关的说法中正确的是( )
 2012年5月6日,天空出现“超级大月亮”,月亮的亮度和视觉直径都大于平常.究其原因,月球的绕地运动轨道实际上是一个偏心率很小的椭圆,当天月球刚好运动到近地点.结合所学知识判断,下列与月球椭圆轨道运动模型有关的说法中正确的是( )
2012年5月6日,天空出现“超级大月亮”,月亮的亮度和视觉直径都大于平常.究其原因,月球的绕地运动轨道实际上是一个偏心率很小的椭圆,当天月球刚好运动到近地点.结合所学知识判断,下列与月球椭圆轨道运动模型有关的说法中正确的是( )| A. | 月球公转周期小于地球同步卫星的公转周期 | |
| B. | 月球在远地点的线速度等于地球第一宇宙速度 | |
| C. | 月球在远地点的加速度小于在近地点的加速度 | |
| D. | 月球在远地点的机械能小于在近地点的机械能 |
16.我国的“玉兔号”月球车于2013年12月14日晚成功降落在月球虹湾区,开始探测科考.机器人“玉兔号”在月球表面做了一个竖直上抛试验,测得物体从月球表面以初速度v0竖直向上抛出上升的最大高度为h,已知月球半径为R,自转周期为T,引力常量为G.则下列说法中正确的是( )
| A. | 月球的平均密度为$\frac{3{{v}_{0}}^{2}}{8πGhR}$ | |
| B. | 月球的第一宇宙速度为v0$\sqrt{\frac{2h}{R}}$ | |
| C. | 月球同步卫星离月球表面高度为$\root{3}{\frac{{{v}_{0}}^{2}R{T}^{2}}{8{π}^{2}h}}$-R | |
| D. | 月球表面重力加速度为$\frac{{{v}_{0}}^{2}}{h}$ |
 用图示的电路可以测定电子的比荷(电子的电荷量与电子质量的比值$\frac{e}{m}$),水平放置的两块平行金属板M、N相距为d,其中N板受紫外线的照射后,将发出沿不同方向运动的光电子,即便是加上反向电压,在电路中也能形成电流,从而引起电流表指针的偏转.若逐渐增大极板间的反向电压,可以发现电流逐渐减小,当电压表示数为U时,电流恰好为零.切断开关,在MN之间加上垂直于纸面的匀强磁场,逐渐增大磁感应强度,当磁感应强度为B时,电流为零.已知紫外线的频率为v,电子的电荷量为e,普朗克常量为h,求:
用图示的电路可以测定电子的比荷(电子的电荷量与电子质量的比值$\frac{e}{m}$),水平放置的两块平行金属板M、N相距为d,其中N板受紫外线的照射后,将发出沿不同方向运动的光电子,即便是加上反向电压,在电路中也能形成电流,从而引起电流表指针的偏转.若逐渐增大极板间的反向电压,可以发现电流逐渐减小,当电压表示数为U时,电流恰好为零.切断开关,在MN之间加上垂直于纸面的匀强磁场,逐渐增大磁感应强度,当磁感应强度为B时,电流为零.已知紫外线的频率为v,电子的电荷量为e,普朗克常量为h,求: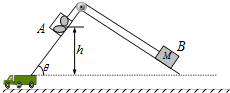 如图所示为仓储公司常采用的“自动化”货物装卸装置,两个相互垂直的斜面固定在平台上,平台跟货车车厢等高,货箱A(含货物)和配重B通过与斜面平行的轻绳跨过光滑滑轮相连.A装载货物后从h=8.0m高处由静止释放,运动到底端时,A和B同时被锁定,卸货后解除锁定,A在B的牵引下被拉回原高度处,再次被锁定.已知θ=53°,B的质量M为1.0×103kg,A、B与斜面间的动摩擦因数均为μ=0.5,滑动摩擦力与最大静摩擦力相等,g取10m/s2,sin53°=0.8,cos53°=0.6.
如图所示为仓储公司常采用的“自动化”货物装卸装置,两个相互垂直的斜面固定在平台上,平台跟货车车厢等高,货箱A(含货物)和配重B通过与斜面平行的轻绳跨过光滑滑轮相连.A装载货物后从h=8.0m高处由静止释放,运动到底端时,A和B同时被锁定,卸货后解除锁定,A在B的牵引下被拉回原高度处,再次被锁定.已知θ=53°,B的质量M为1.0×103kg,A、B与斜面间的动摩擦因数均为μ=0.5,滑动摩擦力与最大静摩擦力相等,g取10m/s2,sin53°=0.8,cos53°=0.6.