题目内容
1.地面上竖直放置一根劲度系数为k,原长为l0的轻质弹簧,在其正上方有一质量为m的小球从A高处自由落到轻质弹簧上,弹簧被压缩,当小球速度最大时,重力势能为$mg({L}_{0}-\frac{mg}{k})$.(以地面为参照平面).分析 小球速度最大时,弹簧所受的弹力等于物块的重力,根据胡克定律求出此时弹簧压缩的长度,根据几何关系求出小球到地面的高度,再求小球具有的重力势能.
解答 解:当小球速度最大时,弹簧所受的弹力等于物块的重力,根据胡克定律得:mg=kx,解得弹簧压缩的长度,:$x=\frac{mg}{k}$,此时小球距地面的高度为:$h={L}_{0}-x={L}_{0}-\frac{mg}{k}$,根据势能表达式得:Ep=mgh=$mg({L}_{0}-\frac{mg}{k})$,
故答案为:$mg({L}_{0}-\frac{mg}{k})$,
点评 本题关键在于确定小球距地面的高度,根据胡克定律求出此时弹簧压缩的长度,根据几何关系求出小球到地面的高度,根据重力势能表达式求解即可.

练习册系列答案
相关题目
11.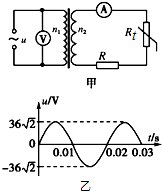 如图甲为理想变压器的示意图,其原、副线圈的匝数比为4:1,电压表和电流表均为理想电表,Rt为阻值随温度升高而变大的热敏电阻,R为定值电阻.若发电机向原线圈输入如图乙所示的正弦交流电,则下列说法正确的是( )
如图甲为理想变压器的示意图,其原、副线圈的匝数比为4:1,电压表和电流表均为理想电表,Rt为阻值随温度升高而变大的热敏电阻,R为定值电阻.若发电机向原线圈输入如图乙所示的正弦交流电,则下列说法正确的是( )
 如图甲为理想变压器的示意图,其原、副线圈的匝数比为4:1,电压表和电流表均为理想电表,Rt为阻值随温度升高而变大的热敏电阻,R为定值电阻.若发电机向原线圈输入如图乙所示的正弦交流电,则下列说法正确的是( )
如图甲为理想变压器的示意图,其原、副线圈的匝数比为4:1,电压表和电流表均为理想电表,Rt为阻值随温度升高而变大的热敏电阻,R为定值电阻.若发电机向原线圈输入如图乙所示的正弦交流电,则下列说法正确的是( )| A. | 变压器副线圈输出电压的有效值为9V | |
| B. | t=0.015s时,发电机的线圈平面与磁场方向垂直 | |
| C. | Rt温度升高时,电流表的示数变小,电压表的读数也变小 | |
| D. | 温度升高时,R的电功率增大 |
12.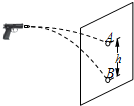 游乐场内两支玩具枪在同一位置先后沿水平方向各射出一颗子弹,打在远处的同一个靶上,A为甲枪子弹留下的弹孔,B为乙枪子弹留下的弹孔,两弹孔在竖直方向上相距高度为h,如图所示,不计空气阻力.关于两枪射出的子弹的初速度大小、飞行时间长短,下列判断正确的是( )
游乐场内两支玩具枪在同一位置先后沿水平方向各射出一颗子弹,打在远处的同一个靶上,A为甲枪子弹留下的弹孔,B为乙枪子弹留下的弹孔,两弹孔在竖直方向上相距高度为h,如图所示,不计空气阻力.关于两枪射出的子弹的初速度大小、飞行时间长短,下列判断正确的是( )
 游乐场内两支玩具枪在同一位置先后沿水平方向各射出一颗子弹,打在远处的同一个靶上,A为甲枪子弹留下的弹孔,B为乙枪子弹留下的弹孔,两弹孔在竖直方向上相距高度为h,如图所示,不计空气阻力.关于两枪射出的子弹的初速度大小、飞行时间长短,下列判断正确的是( )
游乐场内两支玩具枪在同一位置先后沿水平方向各射出一颗子弹,打在远处的同一个靶上,A为甲枪子弹留下的弹孔,B为乙枪子弹留下的弹孔,两弹孔在竖直方向上相距高度为h,如图所示,不计空气阻力.关于两枪射出的子弹的初速度大小、飞行时间长短,下列判断正确的是( )| A. | 乙枪射出的子弹初速度较大 | B. | 两枪射出的子弹初速度一样大 | ||
| C. | 甲枪射出的子弹飞行时间较长 | D. | 乙枪射出的子弹飞行时间较长 |
16. 如图,一固定的半径为R的圆环,均匀带有电量为+Q,将一带电量为-q的试探电荷从无穷远(电势为零)处移至圆环轴线上的O点时电场力对该试探电荷所做的功为4×10-3J,再将其从O点移到P时,需克服电场力做1×10-3J的功,则该试探在该电场的P点时所具有的电势能为( )
如图,一固定的半径为R的圆环,均匀带有电量为+Q,将一带电量为-q的试探电荷从无穷远(电势为零)处移至圆环轴线上的O点时电场力对该试探电荷所做的功为4×10-3J,再将其从O点移到P时,需克服电场力做1×10-3J的功,则该试探在该电场的P点时所具有的电势能为( )
 如图,一固定的半径为R的圆环,均匀带有电量为+Q,将一带电量为-q的试探电荷从无穷远(电势为零)处移至圆环轴线上的O点时电场力对该试探电荷所做的功为4×10-3J,再将其从O点移到P时,需克服电场力做1×10-3J的功,则该试探在该电场的P点时所具有的电势能为( )
如图,一固定的半径为R的圆环,均匀带有电量为+Q,将一带电量为-q的试探电荷从无穷远(电势为零)处移至圆环轴线上的O点时电场力对该试探电荷所做的功为4×10-3J,再将其从O点移到P时,需克服电场力做1×10-3J的功,则该试探在该电场的P点时所具有的电势能为( )| A. | 3×10-3J | B. | 1×10-3J | C. | -3×10-3J | D. | -1×10-3J |
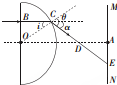 如图所示,MN为竖直放置的光屏,光屏的左侧有半径为R、折射率为$\sqrt{3}$的透明半球体,O为球心,轴线OA垂直于光屏,O至光屏的距离OA=$\frac{3\sqrt{3}}{2}$R.一细束单色光垂直射向半球体的平面,在平面的入射点为B,OB=$\frac{1}{2}$R.求光线在光屏形成的光斑到A点的距离.
如图所示,MN为竖直放置的光屏,光屏的左侧有半径为R、折射率为$\sqrt{3}$的透明半球体,O为球心,轴线OA垂直于光屏,O至光屏的距离OA=$\frac{3\sqrt{3}}{2}$R.一细束单色光垂直射向半球体的平面,在平面的入射点为B,OB=$\frac{1}{2}$R.求光线在光屏形成的光斑到A点的距离.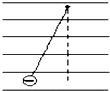 如图所示,一带负电的小球用绝缘细线悬挂在水平方向的电场中处于平衡状态.由图可判定负电的小球受到的电场力方向向左(填“向左”或“向右”).电场的方向向右(填左或右)
如图所示,一带负电的小球用绝缘细线悬挂在水平方向的电场中处于平衡状态.由图可判定负电的小球受到的电场力方向向左(填“向左”或“向右”).电场的方向向右(填左或右)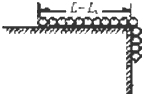 一根长为L的均匀绳索,一部分放在光滑水平桌面上,长为L1=$\frac{L}{4}$的另一部分自然垂在桌面下,如图所示,开始时绳索静止,释放后绳索将沿桌面滑下,求绳索刚滑离桌面时的速度大小.
一根长为L的均匀绳索,一部分放在光滑水平桌面上,长为L1=$\frac{L}{4}$的另一部分自然垂在桌面下,如图所示,开始时绳索静止,释放后绳索将沿桌面滑下,求绳索刚滑离桌面时的速度大小.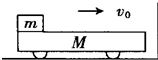 如图所示,一质量M=4kg的小车左端放有一质量m=1kg的铁块,它们以大小v0=4m/s的共同速度沿光滑水平面向竖直墙运动,车与墙碰撞的时间t=0.01s,不计碰撞时机械能的损失,且不计在该时间内铁块速度的变化.铁块与小车之间的动摩擦因数μ=0.5,车长L足够长,铁块不会到达车的右端,最终小车与铁块相对静止.求:
如图所示,一质量M=4kg的小车左端放有一质量m=1kg的铁块,它们以大小v0=4m/s的共同速度沿光滑水平面向竖直墙运动,车与墙碰撞的时间t=0.01s,不计碰撞时机械能的损失,且不计在该时间内铁块速度的变化.铁块与小车之间的动摩擦因数μ=0.5,车长L足够长,铁块不会到达车的右端,最终小车与铁块相对静止.求: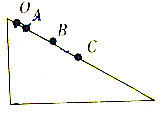 如图所示,将一个小球放在光滑的斜面上,小球从O点由静止开始运动,一次经过斜面上A、B、C点,已知AB=2m,BC=4m,且小球通过AB、BC段的时间相等,小球通过A点的速度v0=1m/s,求:
如图所示,将一个小球放在光滑的斜面上,小球从O点由静止开始运动,一次经过斜面上A、B、C点,已知AB=2m,BC=4m,且小球通过AB、BC段的时间相等,小球通过A点的速度v0=1m/s,求: