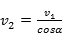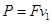题目内容
如图所示,两个内壁光滑、半径不同的半球形碗放在不同高度的水平面上,使两碗口处于同一水平面,现将质量相同的两个小球(小球半径远小于碗的半径),分别从两个碗的边缘由静止释放,当两球分别通过碗的最低点时( )


| A.两球的速度大小相等 |
| B.两球的机械能大小始终相等 |
| C.两球对碗底的压力大小相等 |
| D.小球下滑的过程中重力的功率先增大后减小 |
BCD
试题分析:小球在运动过程中受重力mg和碗的支持力N作用,且支持力N始终不做功,根据动能定理有:mgR=
 -0,解得小球通过碗的最低点时的速度大小为:v=
-0,解得小球通过碗的最低点时的速度大小为:v= ,由于两碗的半径不等,因此两球通过碗的最低点时的速度大小不相等,故选项A错误;整个运动过程中机械能守恒,由于初始时两球质量相等、高度相等,且均由静止释放,因此整个过程中,两球的机械能大小始终相等,故选项B正确;在碗的最低点处,根据牛顿第二定律有:N-mg=
,由于两碗的半径不等,因此两球通过碗的最低点时的速度大小不相等,故选项A错误;整个运动过程中机械能守恒,由于初始时两球质量相等、高度相等,且均由静止释放,因此整个过程中,两球的机械能大小始终相等,故选项B正确;在碗的最低点处,根据牛顿第二定律有:N-mg= ,解得:N=3mg,与碗的半径无关,故选项C正确;根据瞬时功率的计算公式可知,小球下滑的过程中重力的功率为:P=mgvcosα,释放时v=0,通过最低点时cosα=0,而在中间某一位置处mgvcosα≠0,所以小球下滑的过程中重力的功率先增大后减小,故选项D正确。
,解得:N=3mg,与碗的半径无关,故选项C正确;根据瞬时功率的计算公式可知,小球下滑的过程中重力的功率为:P=mgvcosα,释放时v=0,通过最低点时cosα=0,而在中间某一位置处mgvcosα≠0,所以小球下滑的过程中重力的功率先增大后减小,故选项D正确。
练习册系列答案
相关题目
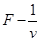 图象(图中AB、BO均为直线)。假设电动车行驶中所受的阻力恒定,下面关于电动车的检测数据说法正确的( )
图象(图中AB、BO均为直线)。假设电动车行驶中所受的阻力恒定,下面关于电动车的检测数据说法正确的( )
 拉细绳,被困人员所受拉力大小为F,此时OA与固定绳OB夹角α,被困人员此时速度为
拉细绳,被困人员所受拉力大小为F,此时OA与固定绳OB夹角α,被困人员此时速度为 。则
。则