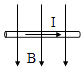题目内容
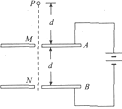
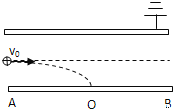
【题目】如图所示,水平放置的平行板电容器,原来两板不带电,上极板接地,极板长L=0.1m,两板间距离d=0.4cm.有一束由相同粒子组成的带电粒子流从两板中央平行于板射入,由于重力作用,粒子能落到下板上,已知粒子质量为m=2×10-6kg,电荷量q=1×10-8C,电容器的电容C=10-6F.不计带电粒子流之间的相互作用,求:
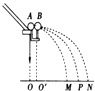
(1)为使第一个粒子能落在下板中点O到紧靠边缘的B点之间,粒子入射速度v应为多大?
(2)以上述速度入射的带电粒子,最多能有多少个落到下极板上?(g取10m/s2)
【答案】(1)2.5m/s ![]() v
v ![]() 5m/s;(2)600个;
5m/s;(2)600个;
【解析】试题分析:(1)第一个粒子在极板间做平抛运动,即
水平位移:x=v0t…①
竖直位移:=at2,…②
由①、②解得:x=v0![]() ;
;
为使第一粒子能落在下板中点O到紧靠边缘的B点之间,x必须满足≤x<L,
即:≤v0![]() <L,解得:即:2.5m/s≤v0≤5m/s;
<L,解得:即:2.5m/s≤v0≤5m/s;
(2)设以上述速度入射的带电粒子,最多能有n个落到下极板上.则第(n+1)个粒子的加速度为a,
由牛顿运动定律得:
mg﹣qE=ma…③
其中E==![]() =
=![]() …④
…④
由③、④得:a=g﹣![]() …⑤
…⑤
第(n+1)粒子做匀变速曲线运动:
x=v0t=L,y=at2,
y=(g﹣![]() )(
)(![]() )2,
)2,
第(n+1)粒子不落到极板上,则y≤,
即:(g﹣![]() )(
)(![]() )2≤,
)2≤,
解得:n=600;

练习册系列答案
相关题目