题目内容
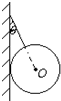 如图所示,将质量分布均匀、重量为G、半径为R的光滑圆球,用长度也为R的细绳拴在竖直墙壁上.要求得绳子对球的拉力FT和墙对球的支持力FN,通常有力的合成、力的分解和正交分解三种方法.请你:
如图所示,将质量分布均匀、重量为G、半径为R的光滑圆球,用长度也为R的细绳拴在竖直墙壁上.要求得绳子对球的拉力FT和墙对球的支持力FN,通常有力的合成、力的分解和正交分解三种方法.请你:(1)画出这三种求解方法的力的图示.在力的合成方法中,要说明合力是哪两个力的合力,在力的分解中,请对重力进行分解;
(2)从三种方法中任选一种方法,解出绳子对球的拉力FT和墙对球的支持力FN的大小.
分析:(1)圆球受到重力G、绳子对球的拉力FT和墙对球的支持力FN,合成法:作出任意两个力的合力,与第三个力等值、反向;分解法:将重力按作用效果进行分解;正交分解法:建立坐标系,将各力分解到相互垂直的两个方向.
(2)根据平衡条件列式,求绳子对球的拉力FT和墙对球的支持力FN的大小.
(2)根据平衡条件列式,求绳子对球的拉力FT和墙对球的支持力FN的大小.
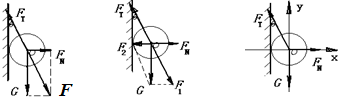
解答:解:(1)力的示意图如下:第一个图是合成法:作出G和支持力FN的合力,与拉力FT等值、反向.
第二个力图是分解法,将重力按作用效果进行分解;
第三个图是正交分解法.
(2)以力的合成为例
从题目所给条件可知,倾角θ=30°,由直角三角形知识可得
FN=Gtanθ=
G
FT=F=
=
答:(1)画出这三种求解方法的力的图示如图.
(2)绳子对球的拉力FT和墙对球的支持力FN的大小分别为:
G和
G.
第二个力图是分解法,将重力按作用效果进行分解;
第三个图是正交分解法.

(2)以力的合成为例
从题目所给条件可知,倾角θ=30°,由直角三角形知识可得
FN=Gtanθ=
| ||
| 3 |
FT=F=
| G |
| cosθ |
2
| ||
| 3 |
答:(1)画出这三种求解方法的力的图示如图.
(2)绳子对球的拉力FT和墙对球的支持力FN的大小分别为:
| ||
| 3 |
2
| ||
| 3 |
点评:力的合成、力的分解和正交分解是处理共点力平衡问题常用的三种方法,要注意它们之间的区别.

练习册系列答案
相关题目
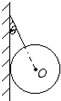 如图所示,将质量分布均匀、重为G的光滑圆球,用细绳拴在竖直墙壁上,已知细绳与竖直墙壁间的夹角为θ.
如图所示,将质量分布均匀、重为G的光滑圆球,用细绳拴在竖直墙壁上,已知细绳与竖直墙壁间的夹角为θ.