题目内容
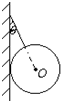
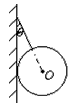
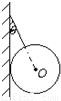
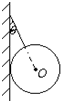
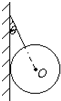 如图所示,将质量分布均匀、重为G的光滑圆球,用细绳拴在竖直墙壁上,已知细绳与竖直墙壁间的夹角为θ.
如图所示,将质量分布均匀、重为G的光滑圆球,用细绳拴在竖直墙壁上,已知细绳与竖直墙壁间的夹角为θ.(1)画出圆球的受力示意图;
(2)求绳子对圆球的拉力大小;
(3)求圆球对墙壁的压力大小.
分析:(1)圆球受到重力G、细绳的拉力T和墙壁的弹力N作用,作出圆球的受力示意图.
(2)(3)根据平衡条件求解绳子对圆球的拉力大小及墙壁对圆球的弹力大小,再由牛顿第三定律求出圆球对墙壁的压力大小.
(2)(3)根据平衡条件求解绳子对圆球的拉力大小及墙壁对圆球的弹力大小,再由牛顿第三定律求出圆球对墙壁的压力大小.
解答: 解:(1)力的示意图如图.
解:(1)力的示意图如图.
(2)根据平衡条件可知,
绳子对圆球的拉力大小 T=
(3)墙壁对圆球的弹力大小N=Gtanθ
由牛顿第三定律:
圆球对墙壁的压力大小.压力大小N′=N=Gtanθ
答:(1)圆球的受力示意图如图;
(2)绳子对圆球的拉力大小为
;
(3)圆球对墙壁的压力大小Gtanθ.
 解:(1)力的示意图如图.
解:(1)力的示意图如图.(2)根据平衡条件可知,
绳子对圆球的拉力大小 T=
| G |
| cosθ |
(3)墙壁对圆球的弹力大小N=Gtanθ
由牛顿第三定律:
圆球对墙壁的压力大小.压力大小N′=N=Gtanθ
答:(1)圆球的受力示意图如图;
(2)绳子对圆球的拉力大小为
| G |
| cosθ |
(3)圆球对墙壁的压力大小Gtanθ.
点评:本题是简单的力平衡问题,关键是分析物体的受力情况,作出受力的示意图,要培养良好的作图习惯.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 如图所示,将质量分布均匀、重量为G、半径为R的光滑圆球,用长度也为R的细绳拴在竖直墙壁上.要求得绳子对球的拉力FT和墙对球的支持力FN,通常有力的合成、力的分解和正交分解三种方法.请你:
如图所示,将质量分布均匀、重量为G、半径为R的光滑圆球,用长度也为R的细绳拴在竖直墙壁上.要求得绳子对球的拉力FT和墙对球的支持力FN,通常有力的合成、力的分解和正交分解三种方法.请你: