题目内容
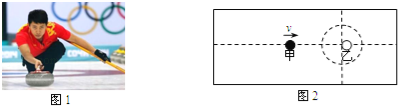
【题目】如图所示,位于竖直面内的曲线轨道的最低点B的切线沿水平方向,且与一位于同一竖直面内、半径R=0.40m的光滑圆形轨道平滑连接。现有一质量m=0.10kg的滑块(可视为质点),从位于轨道上的A点由静止开始滑下,滑块经B点后恰好能通过圆形轨道的最高点C。已知A点到B点的高度h=1.5m,重力加速度g=10m/s2,空气阻力可忽略不计,求:
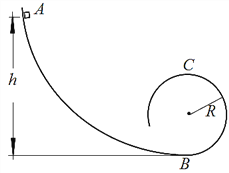
(1)滑块通过C点时的速度大小;
(2)滑块通过圆形轨道B点时对轨道的压力大小;
(3)滑块从A点滑至B点的过程中,克服摩擦阻力所做的功。
【答案】(1) vC=2.0m/s (2) FN′=6.0N (3) Wf =0.50J
【解析】(1)因滑块恰能通过C点,即在C点滑块所受轨道的压力为零,其只受到重力的作用。设滑块在C点的速度大小为vC,根据牛顿第二定律,对滑块在C点有 mg=mvC2/R
解得vC=![]() =2.0m/s
=2.0m/s
(2)设滑块在B点时的速度大小为vB,对于滑块从B点到C点的过程,
根据机械能守恒定律有 ![]() mvB2=
mvB2=![]() mvC2+mg2R
mvC2+mg2R
滑块在B点受重力mg和轨道的支持力FN,根据牛顿第二定律有 FN-mg=mvB2/R
联立上述两式可解得 FN=6mg=6.0N
根据牛顿第三定律可知,滑块在B点时对轨道的压力大小FN′=6.0N
(3)设滑块从A点滑至B点的过程中,克服摩擦阻力所做的功为Wf,对于此过程,
根据动能定律有 mgh-Wf=![]() mvB2
mvB2
解得Wf=mgh-![]() mvB2=0.50J
mvB2=0.50J

练习册系列答案
 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案
相关题目