题目内容
【题目】如图所示,在xoy坐标系内存在一个以(a,0)为圆心、半径为a的圆形磁场区域,方向垂直纸面向里,磁感应强度大小为B.另在y轴右侧有一方向向左的匀强电场,电场强度大小为E,分布于y≥a的范围内.O点为质子源,其出射质子的速度大小相等、方向各异,但质子的运动轨迹均在纸面内.已知质子在磁场中的偏转半径也为a,设质子的质量为m、电量为e,重力及阻力忽略不计.求:
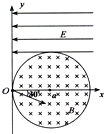
(1)出射速度沿x轴正方向的质子,到达y轴所用的时间;
(2)出射速度与x轴正方向成30°角(如图中所示)的质子,到达y轴时的位置;
(3)质子到达y轴的位置坐标的范围.
【答案】(1)![]() (2)
(2)![]() (3)(a,a+2Ba
(3)(a,a+2Ba![]() )
)
【解析】
试题分析:(1)质子在磁场中做匀速圆周运动,根据洛伦兹力提供向心力得:![]()
即:![]()
出射速度沿x轴正方向的质子,经![]() 圆弧后以速度v垂直于电场方向进入电场,在磁场中运动的时间为:
圆弧后以速度v垂直于电场方向进入电场,在磁场中运动的时间为:
![]()
质子进入电场后做类平抛运动,沿电场方向运动a后到达y轴,由匀变速直线运动规律有:![]()
即:![]()
故所求时间为:![]()
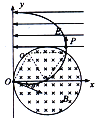
(2)质子转过120°角后离开磁场,再沿直线到达图中P点,最后垂直电场方向进入电场,做类平抛运动,并到达y轴,运动轨迹如图中所示.
由几何关系可得P点距y轴的距离为:x1=a+asin30°=1.5a
设在电场中运动的时间为 t3,由匀变速直线运动规律有:![]()
即 ![]()
质子在y轴方向做匀速直线运动,到达y轴时有:![]()
所以质子在y轴上的位置为:![]()
(3)若质子在y轴上运动最远,应是质子在磁场中沿右边界向上直行,垂直进入电场中做类平抛运动,
此时x′=2a
质子在电场中在y方向运动的距离为:![]()
质子离坐标原点的距离为:![]()
由几何关系可证得,此题中凡进入磁场中的粒子,从磁场穿出时速度方向均与y轴平行,且只有进入电场中的粒子才能打到y轴上,因此
质子到达y轴的位置坐标的范围应是(a,a+2Ba![]() )
)

 口算题天天练系列答案
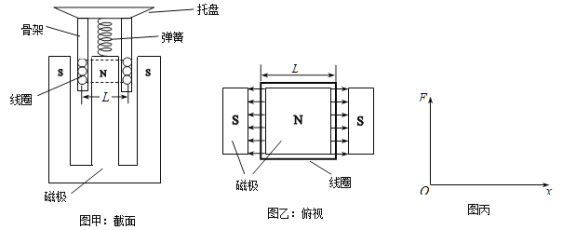
口算题天天练系列答案【题目】用如图所示的气垫导轨装置验证系统的机械能守恒;在气垫导轨上安装了两光电门12,在滑块上固定一竖直遮光条,滑块用细线绕过定滑轮与钩码相连;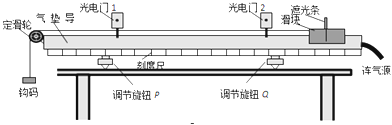
(1)在调整气垫导轨水平时.滑块不挂钩码和细线,接通气源后,给滑块一个初速度,使它从轨道右端向左运动,发现滑块通过光电门1的时间小于通过光电门2的时间.下列能够实现调整导轨水平的措施是 ;
A.调节气垫导轨使左端升高一些 |
B.调节气垫导轨使左端降低一些 |
C.遮光条的宽度应该适当大一些 |
D.滑块的质量增大一些 |
(2)试验时,测出光电门1、2间的距离L,遮光条的宽度d,滑块和遮光条的总质量M,钩码质量m.由数字计时器读出遮光条通过光电门的时间间隔为△t,则滑块通过光电门的速度表达式为 ;若用v1、v2表示通过光电门1、2的速度,则系统机械能守恒成立的表达式 ;