题目内容
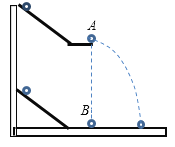
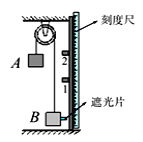
【题目】如图所示,长为L的轻杆两端分别固定有质量均为m的A、B两小铁球,杆的三等分点O处有光滑的水平固定转轴,使轻杆可绕转轴在竖直面内无摩擦转动。用手将该装置固定在杆恰好水平的位置,然后由静止释放。重力加速度为g。求
(1)当杆到达竖直位置时,小球A的速度![]() 和杆对小球B的弹力;
和杆对小球B的弹力;
(2)从释放轻杆到轻杆转到竖直位置过程中,轻杆对小球A做的功。

【答案】(1)![]() ,弹力大小为
,弹力大小为![]() ,方向竖直向上;(2)
,方向竖直向上;(2)![]()
【解析】试题分析(1)对整个系统而言,由于只有重力做功,所以系统的机械能守恒.由系统的机械能守恒和速度关系求出杆到达竖直位置时两球的角速度,根据![]() 求得AB的速度,在竖直位置对B由牛顿第二定律可以求出杆对小球B的弹力;(2)根据动能定理求得杆对A做功。
求得AB的速度,在竖直位置对B由牛顿第二定律可以求出杆对小球B的弹力;(2)根据动能定理求得杆对A做功。
(1)当杆到达竖直位置时,设A、B的速度分别为![]()
因为A、B角速度相同,所以:![]()
由系统机械能守恒得:![]()
联立解得:![]()
![]()
在竖直位置时对B由牛顿第二定律得:![]()
解得:![]()
即杆对B的弹力大小为![]() ,方向竖直向上
,方向竖直向上
(2)对A由动能定理得:![]()
解得:![]()

练习册系列答案
相关题目