题目内容
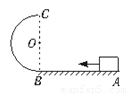
如图所示,滑块在恒定外力F= 3mg/2作用下从水平轨道上的A点由静止出发到B点时撤去外力,又沿竖直面内的半径为R光滑半圆形轨道运动,且恰好通过轨道最高点C,滑块脱离半圆形轨道后又刚好落到原出发点A,滑块与地面的摩擦因数为0.25,试求
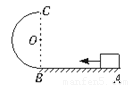
(1)滑块运动到B点速度大小
(2)滑块在半圆形轨道上运动时,对轨道压力的最小值和最大值
【答案】
(1) a=5g/4 (2) 最小值F N=0 N 最大压力为6mg
【解析】
试题分析:设圆周的半径为R,则在C点:
mg=m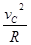
最小值F N=0 N ①
离开C点,滑块做平抛运动,则2R=gt2/2 ②
v C t =sAB ③
由牛顿第二定律 F-f =ma
a=5g/4
由A到B运动过程:
vB2=2asAB
VB= 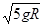
由牛顿第二定律FN-mg=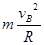 ;
;
∴FN=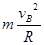 +mg=6mg
+mg=6mg
由牛顿第三定律得:滑块对轨道的最大压力为6mg
考点:动能定理的应用;牛顿第二定律;平抛运动;向心力.
点评:本题注意应分段分析,不同的过程采用不同的物理规律求解,特别要注意在竖直面上的圆周运动中的临界值的确定.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
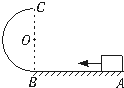 如图所示,滑块在恒定外力F=1.5mg的作 用下从水平轨道上的A点由静止出发到B点时撤去外力,又沿竖直面内的光滑半圆形轨道运动,且恰好通过轨道最高点C,滑块脱离半圆形轨道后又刚好落到原出发点A,求AB段与滑块间的动摩擦因数.
如图所示,滑块在恒定外力F=1.5mg的作 用下从水平轨道上的A点由静止出发到B点时撤去外力,又沿竖直面内的光滑半圆形轨道运动,且恰好通过轨道最高点C,滑块脱离半圆形轨道后又刚好落到原出发点A,求AB段与滑块间的动摩擦因数.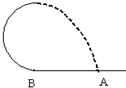 (2011?许昌一模)如图所示,滑块在恒定外力作用下从水平轨道上的A点由静止出发,到B点时撤去外力,又沿竖直面内的半月形轨道运动,且恰好通过轨道最高点C,滑块脱离半圆形轨道后又刚好落到原出发点A,试求滑块在AB段运动过程中的加速度.重力加速度为g.
(2011?许昌一模)如图所示,滑块在恒定外力作用下从水平轨道上的A点由静止出发,到B点时撤去外力,又沿竖直面内的半月形轨道运动,且恰好通过轨道最高点C,滑块脱离半圆形轨道后又刚好落到原出发点A,试求滑块在AB段运动过程中的加速度.重力加速度为g. 如图所示,滑块在恒定外力F=2mg的作用下,从水平轨道上的A点由静止出发运动到B点时撤去外力,又沿竖直面内的半径为R的光滑半圆形轨道运动,且恰好通过轨道最高点C,滑块脱离半圆形轨道后又刚好落到原出发点A,求
如图所示,滑块在恒定外力F=2mg的作用下,从水平轨道上的A点由静止出发运动到B点时撤去外力,又沿竖直面内的半径为R的光滑半圆形轨道运动,且恰好通过轨道最高点C,滑块脱离半圆形轨道后又刚好落到原出发点A,求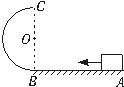 如图所示,滑块在恒定外力F作用下从水平轨道上的A点由静止出发到B点时撤去外力,又沿竖直面内的光滑半圆形轨道运动,且恰能通过轨道最高点C,AB距离为S,轨道半径为R,求滑块在AB段运动过程中的动摩擦因数.
如图所示,滑块在恒定外力F作用下从水平轨道上的A点由静止出发到B点时撤去外力,又沿竖直面内的光滑半圆形轨道运动,且恰能通过轨道最高点C,AB距离为S,轨道半径为R,求滑块在AB段运动过程中的动摩擦因数.