题目内容
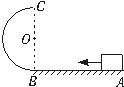 如图所示,滑块在恒定外力F作用下从水平轨道上的A点由静止出发到B点时撤去外力,又沿竖直面内的光滑半圆形轨道运动,且恰能通过轨道最高点C,AB距离为S,轨道半径为R,求滑块在AB段运动过程中的动摩擦因数.
如图所示,滑块在恒定外力F作用下从水平轨道上的A点由静止出发到B点时撤去外力,又沿竖直面内的光滑半圆形轨道运动,且恰能通过轨道最高点C,AB距离为S,轨道半径为R,求滑块在AB段运动过程中的动摩擦因数.分析:物块恰好通过最高点C,知在C点重力提供圆周运动的向心力.由B到C过程运用机械能守恒定律可求出B点的动能,再对AB段运用动能定理求出动摩擦因数μ.
解答:解:在C点:mg=m
vc=
由B到C过程重力做功:-2mgR=
m
-
m
vB=
由A到B运动过程:(F-μmg)s=
m
μ=
-
答:滑块在AB段运动过程中的动摩擦因数为
-
.
| vC2 |
| R |
vc=
| Rg |
由B到C过程重力做功:-2mgR=
| 1 |
| 2 |
| v | 2 c |
| 1 |
| 2 |
| v | 2 B |
vB=
| 5Rg |
由A到B运动过程:(F-μmg)s=
| 1 |
| 2 |
| v | 2 B |
μ=
| F |
| mg |
| 5R |
| 2S |
答:滑块在AB段运动过程中的动摩擦因数为
| F |
| mg |
| 5R |
| 2S |
点评:本题综合运用了动能定理、机械能守恒定律和牛顿第二定律,运用动能定理和机械能守恒定律时,一定要选择合适的研究过程.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
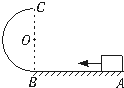 如图所示,滑块在恒定外力F=1.5mg的作 用下从水平轨道上的A点由静止出发到B点时撤去外力,又沿竖直面内的光滑半圆形轨道运动,且恰好通过轨道最高点C,滑块脱离半圆形轨道后又刚好落到原出发点A,求AB段与滑块间的动摩擦因数.
如图所示,滑块在恒定外力F=1.5mg的作 用下从水平轨道上的A点由静止出发到B点时撤去外力,又沿竖直面内的光滑半圆形轨道运动,且恰好通过轨道最高点C,滑块脱离半圆形轨道后又刚好落到原出发点A,求AB段与滑块间的动摩擦因数.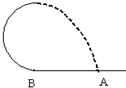 (2011?许昌一模)如图所示,滑块在恒定外力作用下从水平轨道上的A点由静止出发,到B点时撤去外力,又沿竖直面内的半月形轨道运动,且恰好通过轨道最高点C,滑块脱离半圆形轨道后又刚好落到原出发点A,试求滑块在AB段运动过程中的加速度.重力加速度为g.
(2011?许昌一模)如图所示,滑块在恒定外力作用下从水平轨道上的A点由静止出发,到B点时撤去外力,又沿竖直面内的半月形轨道运动,且恰好通过轨道最高点C,滑块脱离半圆形轨道后又刚好落到原出发点A,试求滑块在AB段运动过程中的加速度.重力加速度为g. 如图所示,滑块在恒定外力F=2mg的作用下,从水平轨道上的A点由静止出发运动到B点时撤去外力,又沿竖直面内的半径为R的光滑半圆形轨道运动,且恰好通过轨道最高点C,滑块脱离半圆形轨道后又刚好落到原出发点A,求
如图所示,滑块在恒定外力F=2mg的作用下,从水平轨道上的A点由静止出发运动到B点时撤去外力,又沿竖直面内的半径为R的光滑半圆形轨道运动,且恰好通过轨道最高点C,滑块脱离半圆形轨道后又刚好落到原出发点A,求