题目内容
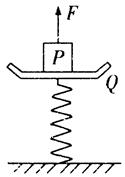
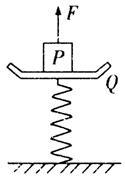
一个弹簧秤放在水平面上,Q为与轻弹簧上端连在一起的秤盘,P为一重物.已知P的质量M=10.5 kg,Q质量m=1.5 kg,弹簧的质量不计,劲度系数k=800 N/m,系统处于静止,如图所示.现给P施加一个方向竖直向上的力F,使它从静止开始向上做匀加速运动,已知在前0.2 s时间内,F为变力,0.2 s以后,F为恒力.求力F的最大值与最小值.(g取10 m/s2)
解析:(1)P做匀加速运动,它受到的合外力一定是恒力,P受到的外力共有3个,即重力Mg、向上的力F及Q对P的支持力FN,其中Mg为恒力,FN为变力.题目说0.2 s以后F为恒力,说明t=0.2 s的时刻,正是P与Q开始脱离接触的时间,即临界点.
(2)t=0.2 s的时刻,是Q对P的作用力FN恰好减为零的时刻,此时刻P与Q具有相同的速度及加速度,因此,此时刻弹簧并未恢复原长,也不能认为此时刻弹簧的弹力为零.
(3)当t=0时刻,应是力F最小的时刻,此时刻F小=(M+m)a(a为它们的加速度),随后,由于弹簧弹力逐渐变小,而P与Q受到的合力保持不变,因此力F逐渐变大,至t=0.2 s时F增至最大,此时刻F大=M(a+g).解答过程如下:
设开始时弹簧压缩量为x1,且t=0.2 s时弹簧的压缩量为x2,物体P的加速度为a,则有
kx1=(M+m)g ①
kx2-mg=ma ②
x1-x2=![]() at2 ③
at2 ③
由①式,x1=![]() =0.15 m
=0.15 m
解②③式,a=6 m/s2
所以F小=(M+m)a=72 N
F大=M(a+g)=168 N.
答案:Fmin=72 N Fmax=168 N

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
 一个弹簧秤放在水平地面上,Q为与轻弹簧上端连在一起的秤盘,P为重物,已知P的质量M=10.5kg,Q 的质量m=1.5kg,弹簧的质量不计,劲度系数k=800N/m,系统处于静止.如图所示,现给P施加一个方向竖直向上的力F,使它从静止开始向上做匀加速运动,已知在前0.2s内,F为变力,0.2s以后,F为恒力.
一个弹簧秤放在水平地面上,Q为与轻弹簧上端连在一起的秤盘,P为重物,已知P的质量M=10.5kg,Q 的质量m=1.5kg,弹簧的质量不计,劲度系数k=800N/m,系统处于静止.如图所示,现给P施加一个方向竖直向上的力F,使它从静止开始向上做匀加速运动,已知在前0.2s内,F为变力,0.2s以后,F为恒力. (2011?泗阳县一模)一个弹簧秤放在水平地面上,Q为与轻弹簧上端连在一起的秤盘,P为重物,已知P的质量M=10.5kg,Q的质量 m=1.5kg,弹簧的质量不计,劲度系数 k=800N/m,系统处于静止.如图所示,现给P施加一个方向竖直向上的力F,使它从静止开始向上做匀加速运动,则在向上运动的过程中力F随时间变化的图象是( )
(2011?泗阳县一模)一个弹簧秤放在水平地面上,Q为与轻弹簧上端连在一起的秤盘,P为重物,已知P的质量M=10.5kg,Q的质量 m=1.5kg,弹簧的质量不计,劲度系数 k=800N/m,系统处于静止.如图所示,现给P施加一个方向竖直向上的力F,使它从静止开始向上做匀加速运动,则在向上运动的过程中力F随时间变化的图象是( )