题目内容
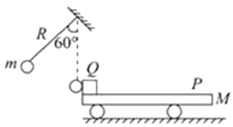
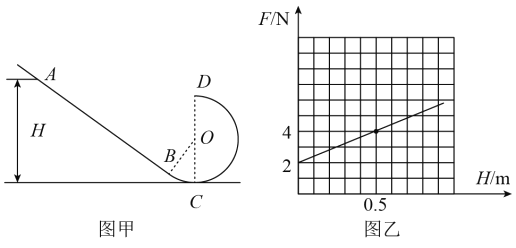
【题目】如图甲所示，竖直平面内的光滑轨道由倾斜直轨道AB和圆轨道BCD组成，AB和BCD相切于B点，OB与OC夹角为37
，CD连线是圆轨道竖直方向的直径
、D为圆轨道的最低点和最高点
，可视为质点的小滑块从轨道AB上高H处的某点由静止滑下，用力传感器测出滑块经过圆轨道最低点C时对轨道的压力为F，并得到如图乙所示的压力F与高度H的关系图象，该图线截距为2N，且过
点
取
求：
滑块的质量和圆轨道的半径；
若要求滑块不脱离圆轨道，则静止滑下的高度为多少；
是否存在某个H值，使得滑块经过最高点D飞出后落在圆心等高处的轨道上若存在，请求出H值；若不存在，请说明理由．
【答案】（1）m=0.2kg ,1m （2）
（3）
【解析】
当
时，由图象截距可知
当小物块从A点静止下滑，由图象知，
，对轨道的压力
解得
．
不脱离轨道分两种情况：
①到圆心等高处速度为零
有能量守恒可知，滑块从静止开始下滑高度
②通过最高点，通过最高点的临界条件
设下落高度为
，
由动能定理
解得
则应该满足下落高度
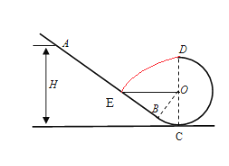
假设滑块经过最高点D后能直接落到直轨道AB上与圆心等高的E点：
解得：
而滑块过D点的临界速度
由于：
，所以存在一个H值，使得滑块经过最高点D后能直接落到直轨道AB上与圆心等高的点
解得：
练习册系列答案
相关题目
