题目内容
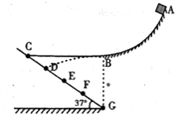 如图所示,AB是光滑的斜槽,斜槽的末端B的切线水平,斜面CG的倾角θ=37°,斜面上的C点与B点在同一水平面上,G点与B点在同一竖直线上,D、E、F是光滑斜面 CG上的四等分点.现有一个质量为1kg的小物体在离B端高h=5m的A处,由静止开始沿 斜槽滑下,恰好落到斜面上的D点,物体落到D点后不再反弹,只有沿斜面方向上的速度.sin37°=0.6,cos37°=0.8,g=10m/s2.则:
如图所示,AB是光滑的斜槽,斜槽的末端B的切线水平,斜面CG的倾角θ=37°,斜面上的C点与B点在同一水平面上,G点与B点在同一竖直线上,D、E、F是光滑斜面 CG上的四等分点.现有一个质量为1kg的小物体在离B端高h=5m的A处,由静止开始沿 斜槽滑下,恰好落到斜面上的D点,物体落到D点后不再反弹,只有沿斜面方向上的速度.sin37°=0.6,cos37°=0.8,g=10m/s2.则:(1)物体到达B点的速度大小是多少?
(2)物体落到斜面CG上时,损失的机械能是多少?
分析:(1)物体从A到B的过程中,运用机械能守恒定律即可求得到达B点的速度;
(2)从B点抛出后做平抛运动,根据平抛运动额规律求出CD之间的距离及到达D点时,在竖直方向的速度,根据速度的分解原则求出沿斜面向下的速度,根据能量守恒求出物体落到斜面CG上时,损失的机械能.
(2)从B点抛出后做平抛运动,根据平抛运动额规律求出CD之间的距离及到达D点时,在竖直方向的速度,根据速度的分解原则求出沿斜面向下的速度,根据能量守恒求出物体落到斜面CG上时,损失的机械能.
解答:解:(1)物体从A到B的过程中,由机械能守恒定律得:
mgh=
mvB2
解得:vB=10m/s
(2)设CD之间的距离为L,物体从B到D所用的时间为t,则从B点抛出后,
在水平方向上有:3Lcos37°=vBt
竖直方向有:Lsin37°=
gt2
解得:t=0.5s,L=
m
到达D点时,在竖直方向的速度为vy=gt
所以,物体到达D点后沿斜面方向的分速度为vD=vBcos37°-vysin37°=5m/s
根据能力守恒得:
mvB2+mgLsin37°=Q+
mvD2
解得:Q=50J
答:(1)物体到达B点的速度大小是10m/s;
(2)物体落到斜面CG上时,损失的机械能为50J.
mgh=
| 1 |
| 2 |
解得:vB=10m/s
(2)设CD之间的距离为L,物体从B到D所用的时间为t,则从B点抛出后,
在水平方向上有:3Lcos37°=vBt
竖直方向有:Lsin37°=
| 1 |
| 2 |
解得:t=0.5s,L=
| 25 |
| 12 |
到达D点时,在竖直方向的速度为vy=gt
所以,物体到达D点后沿斜面方向的分速度为vD=vBcos37°-vysin37°=5m/s
根据能力守恒得:
| 1 |
| 2 |
| 1 |
| 2 |
解得:Q=50J
答:(1)物体到达B点的速度大小是10m/s;
(2)物体落到斜面CG上时,损失的机械能为50J.
点评:本题主要考查了机械能守恒定律、平抛运动的基本规律的应用,注意物体落到D点后不再反弹,说明只有沿着斜面方向的速度,要能根据速度的分解原则求出沿斜面的速度,难度适中.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图所示,AB是在竖直平面内的1/4圆周的光滑圆弧轨道,过圆弧轨道下端边缘B点的切线是水平的,B点距正下方水平地面上C点的距离为h.一质量为m的小物块(可视为质点)自A点由静止释放,并从B点水平飞出,最后落到水平地面上的D点.已知小物块落地点D到C点的距离为x,重力加速度为g,空气阻力可忽略不计,求:
如图所示,AB是在竖直平面内的1/4圆周的光滑圆弧轨道,过圆弧轨道下端边缘B点的切线是水平的,B点距正下方水平地面上C点的距离为h.一质量为m的小物块(可视为质点)自A点由静止释放,并从B点水平飞出,最后落到水平地面上的D点.已知小物块落地点D到C点的距离为x,重力加速度为g,空气阻力可忽略不计,求: 如图所示,abc是光滑的轨道,其中ab是水平的,bc为与ab相切的位于竖直平面内的半圆,半径R=O.30m.质量m=0.20kg的小球A静止在轨道上,另一质量M=O.60kg、速度V0=5.5m/s的小球B与小球A正碰.已知相碰后小球A经过半圆的最高点c落到轨道上距b点为,
如图所示,abc是光滑的轨道,其中ab是水平的,bc为与ab相切的位于竖直平面内的半圆,半径R=O.30m.质量m=0.20kg的小球A静止在轨道上,另一质量M=O.60kg、速度V0=5.5m/s的小球B与小球A正碰.已知相碰后小球A经过半圆的最高点c落到轨道上距b点为, (2005?河东区二模)如图所示,AB是一段位于竖起平面内的光滑轨道,高度为h,未端B处的切线方向水平.一个小物体P从轨道顶端A点由静止释放,滑到B端后飞出,落到地面上的C点,轨迹如图中虚线BC所示.已知它的落点相对于B点的水位移OC=L,现在轨道下紧贴B安放一水平板,板右端与B点的水平距离为
(2005?河东区二模)如图所示,AB是一段位于竖起平面内的光滑轨道,高度为h,未端B处的切线方向水平.一个小物体P从轨道顶端A点由静止释放,滑到B端后飞出,落到地面上的C点,轨迹如图中虚线BC所示.已知它的落点相对于B点的水位移OC=L,现在轨道下紧贴B安放一水平板,板右端与B点的水平距离为 