题目内容
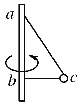
【题目】如图所示,A、B两小球分别连在轻绳两端,B球另一端用弹簧固定在倾角为30°的光滑斜面上.A、B两小球的质量分别为mA、mB,重力加速度为g,若不计弹簧质量,在绳被剪断瞬间,A、B两球的加速度大小分别为( )

A. 都等于g/2
B. g/2 和mAg/2mB
C. g/2 和0
D. 0和mBg/2mA
【答案】B
【解析】
在剪短上端的绳子的瞬间,绳子上的拉力立即减为零,而弹簧的伸长量没有来得及发生改变,故弹力不变,再分别对A、B两个小球运用牛顿第二定律,即可求得加速度。
对A:在剪断绳子之前,A处于平衡状态,所以弹簧的拉力等于A的重力沿斜面的分力相等.在剪断绳子的瞬间,绳子上的拉力立即减为零,此时小球A受到的合力为F=mgsin30°=ma,![]()
对B:在剪断绳子之前,对B球进行受力分析,B受到重力、弹簧对它斜向上的拉力、支持力及绳子的拉力,在剪断绳子的瞬间,绳子上的拉力立即减为零,对B球进行受力分析,则B受到到重力、弹簧的向上拉力、支持力.所以根据牛顿第二定律得:mAgsin30°=mBa
解得:![]()
故B正确。

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目