题目内容
1.如图甲所示,一个倾角θ=37°足够长的粗糙斜面固定在地面上,一滑块从底端A点滑上斜面,初速度v0=8m/s,滑块滑至B点后又返回到A点.滑块运动的v-t图象如图乙所示,求:(已知:sin37°=0.6,cos37°=0.8,重力加速度g=10m/s2)(1)AB之间的距离;
(2)滑块回到A点时的速度大小.

分析 根据速度时间图线与时间轴围成的面积求出AB之间的距离.根据速度位移公式求出上滑时的加速度,结合牛顿第二定律求出摩擦力,再根据牛顿第二定律求出下滑的加速度,从而根据速度位移公式求出再次回到A点的速度.
解答 解:(1)图线与时间轴围成的面积表示位移,则AB间的距离为:
x=$\frac{1}{2}×1×8$=4m.
(2)根据速度位移公式知,匀减速上滑的加速度大小为:
${a}_{1}=\frac{{{v}_{0}}^{2}}{2x}=\frac{1{6}^{2}}{2×16}=8m/{s}^{2}$,
根据牛顿第二定律得:
f+mgsin37°=ma1,
解得滑动摩擦力为:
f=ma1-mgsin37°,
则滑块下滑的加速度为:
${a}_{2}=\frac{mgsin37°-f}{m}=\frac{2mgsin37°-m{a}_{1}}{m}$=$2gsin37°-{a}_{1}=12-8m/{s}^{2}=4m/{s}^{2}$,
滑块再次回到A点的速度为:
v=$\sqrt{2{a}_{2}x}$=$\sqrt{2×4×4}$=4$\sqrt{2}$m/s.
答:(1)AB之间的距离为4m;
(2)滑块再次回到A点时的速度为4$\sqrt{2}$m/s.
点评 本题考查了牛顿第二定律和运动学公式的综合运用,知道加速度是联系力学和运动学的桥梁,并掌握v-t图象的正确应用.

练习册系列答案
相关题目
11.下列说法中正确的是( )
| A. | 伽利略猜想自由落体的运动速度与下落时间成正比,并直接用实验进行了验证 | |
| B. | 牛顿第一定律、牛顿第二定律都可以通实验来验证 | |
| C. | 单位m、kg、s是一组属于国际单位制的基本单位 | |
| D. | 用比值法定义的物理概念在物理学中占有相当的比例,例如加速度a=$\frac{F}{m}$就是采用比值定义法 |
12. 将一个质量为m的小球,从同一高度h以相同大小的初速度分别沿竖直方向下落、沿光滑斜面下滑、水平抛出,最后落到同一水平面内,如图所示,不计空气阻力,小球沿上述三条不同的路径运动时,下列说法正确的是( )
将一个质量为m的小球,从同一高度h以相同大小的初速度分别沿竖直方向下落、沿光滑斜面下滑、水平抛出,最后落到同一水平面内,如图所示,不计空气阻力,小球沿上述三条不同的路径运动时,下列说法正确的是( )
 将一个质量为m的小球,从同一高度h以相同大小的初速度分别沿竖直方向下落、沿光滑斜面下滑、水平抛出,最后落到同一水平面内,如图所示,不计空气阻力,小球沿上述三条不同的路径运动时,下列说法正确的是( )
将一个质量为m的小球,从同一高度h以相同大小的初速度分别沿竖直方向下落、沿光滑斜面下滑、水平抛出,最后落到同一水平面内,如图所示,不计空气阻力,小球沿上述三条不同的路径运动时,下列说法正确的是( )| A. | 三种情况重力做功的平均功率一样大 | |
| B. | 三种情况落地时的速度大小相等 | |
| C. | 三种情况从抛出到落地运动时间相同 | |
| D. | 三种情况重力做功一样多 |
9.下面叙述符合物理学史实的是( )
| A. | 伽利略通过理想实验总结出了惯性定律 | |
| B. | 亚里士多德发现忽略空气阻力,重物与轻物下落得同样快 | |
| C. | 开普勒通过研究行星观测记录,发现了行星运动三大定律 | |
| D. | 牛顿发现了万有引力定律并测出了引力常量 |
16.2014年10月24日2点00分,我国自行研制的探月工程三期返回飞行试验器,在西昌卫星发射中心用长征三号丙运载火箭发射升空.若返回飞行试验器变轨后沿圆形轨道环绕月球运行,运行周期为T.已知月球半径为R,月球表面的重力加速度为g.则飞船离月球表面的高度为( )
| A. | $\root{3}{\frac{g{R}^{2}{T}^{2}}{4{π}^{2}}}$-R | B. | $\root{3}{\frac{gR{T}^{2}}{4{π}^{2}}}$-R | C. | $\root{3}{\frac{G{R}^{2}{T}^{2}}{4{π}^{2}}}$-R | D. | $\root{3}{\frac{g{R}^{2}T}{4{π}^{2}}}$-R |
6.下列说法中正确的是( )
| A. | 布朗运动是悬浮的固体微粒的运动,反映了液体分子的无规则运动 | |
| B. | 悬浮在液体中的固体颗粒越大,布朗运动越显著 | |
| C. | 扩散现象是物质分子永不停息地做无规则运动的证明 | |
| D. | 因为布朗运动的剧烈程度跟温度有关,所以布朗运动也可以叫做热运动 |
13. 在如图所示电路中,A、B是两只相同的小灯泡,L是一个带铁芯的线圈,线圈的电阻忽略不计.调节滑动变阻器R,使电路稳定时两只灯泡都正常发光,则下列说法中正确的是( )
在如图所示电路中,A、B是两只相同的小灯泡,L是一个带铁芯的线圈,线圈的电阻忽略不计.调节滑动变阻器R,使电路稳定时两只灯泡都正常发光,则下列说法中正确的是( )
 在如图所示电路中,A、B是两只相同的小灯泡,L是一个带铁芯的线圈,线圈的电阻忽略不计.调节滑动变阻器R,使电路稳定时两只灯泡都正常发光,则下列说法中正确的是( )
在如图所示电路中,A、B是两只相同的小灯泡,L是一个带铁芯的线圈,线圈的电阻忽略不计.调节滑动变阻器R,使电路稳定时两只灯泡都正常发光,则下列说法中正确的是( )| A. | 合上S时,B灯先亮,A灯逐渐亮起来 | |
| B. | 合上S时,A灯和B灯立即达到正常发光状态 | |
| C. | 断开S时,A、B两灯都不会立即熄灭,通过A、B两灯的电流方向都与原电流方向相同 | |
| D. | 断开S时,A灯会突然闪亮一下再熄灭 |
10.下列说法正确的是( )
| A. | 理想气体的温度变化时,其分子平均动能和分子势能也随之改变 | |
| B. | 气体压强本质上是大量气体作用在器壁单位面积上的平均作用力 | |
| C. | 机械能不可能全部转化为内能,内能也不可能全部转化为机械能 | |
| D. | 一等质量的类型气体经历等容过程,如果吸热,则其内能一定增加 | |
| E. | 热量能够自发第从高温物体传递到低温物体,但不能自发地从低温物体传递到高温物体 |
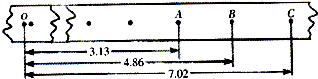 在利用自由落体“验证机械能守恒定律”的实验中:
在利用自由落体“验证机械能守恒定律”的实验中: