题目内容
18. 如图所示,C点下方通过细线悬挂一质量为m的重物,则AC线受到的拉力大小为$\frac{4}{3}$mg;BC杆受到的作用力的大小为$\frac{5}{3}$mg,方向沿C→B(sin37°=0.6,sin53°=0.8)
如图所示,C点下方通过细线悬挂一质量为m的重物,则AC线受到的拉力大小为$\frac{4}{3}$mg;BC杆受到的作用力的大小为$\frac{5}{3}$mg,方向沿C→B(sin37°=0.6,sin53°=0.8)
分析 将重物对C的拉力F按作用效果进行分解,由平行四边形定则作出分力,再由数学知识求解.
解答  解:重物静止时对C点的拉力 F=mg
解:重物静止时对C点的拉力 F=mg
将重物对C的拉力F沿AC方向和BC方向进行分解,由平行四边形定则作出分力,如图,则得
TAC=Fcot37°=$\frac{4}{3}$mg
TBC=$\frac{F}{sin37°}$=$\frac{5}{3}$mg
则得,AC线受到的拉力大小为$\frac{4}{3}$mg;BC杆受到的作用力的大小为$\frac{5}{3}$mg,方向沿C→B.
故答案为:$\frac{4}{3}$mg;$\frac{5}{3}$mg;C→B.
点评 本题运用分解法解决共点力平衡问题,也可以由力的合成法或正交分解法研究.

练习册系列答案
相关题目
8.关于物体的重心,下列说法正确的是( )
| A. | 重心就是物体内最重的一点 | |
| B. | 重心从效果上看是物体各部分所受重力作用集中于一点 | |
| C. | 任何形状规则的物体,它的重心一定在其几何中心 | |
| D. | 重心不可能在物体外 |
6.在同一地点,质量不同的两个物体从同一高度同时开始做自由落体运动,则( )
| A. | 质量大的物体先落地 | B. | 质量小的物体先落地 | ||
| C. | 两个物体同时落地 | D. | 质量大的物体下落的加速度小 |
9.某同学用如图1所示的装置探究小车加速度与合外力的关系.图中小车A左端连接一纸带并穿过打点计时器B的限位孔,右端用一轻绳绕过滑轮系于拉力传感器C的下端,A、B置于水平放置的一端带有定滑轮的足够长的木板上.不计绳与滑轮的摩擦及滑轮的质量.实验时,先接通电源再释放小车,打点计时器在纸带上打下一系列点.该同学在保证小车A质量不变的情况下,通过改变P的质量来改变小车A所受的外力,由传感器和纸带测得的拉力F和加速度a数据如下表所示.
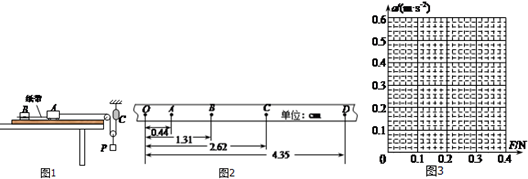
(1)第4次实验得到的纸带如图2所示,O、A、B、C和D是纸带上的五个计数点,每两个相邻点间有四个点没有画出,A、B、C、D四点到O点的距离如图.打点计时器电源频率为50Hz.根据纸带上数据计算出小车加速度a为0.43m/s2.
(2)在实验中,不需要(选填“需要”或“不需要”)满足重物P的质量远小于小车A的质量.
(3)根据表中数据,在图3所示坐标系中做出小车加速度a与力F的关系图象.
(4)根据图象推测,实验操作中重要的疏漏是没有平衡摩擦力或者摩擦力平衡不足.

| 次数 | 1 | 2 | 3 | 4 | 5 |
| F/N | 0.10 | 0.18 | 0.26 | 0.30 | 0.40 |
| a/(m•s-2) | 0.08 | 0.22 | 0.37 | 0.59 |
(2)在实验中,不需要(选填“需要”或“不需要”)满足重物P的质量远小于小车A的质量.
(3)根据表中数据,在图3所示坐标系中做出小车加速度a与力F的关系图象.
(4)根据图象推测,实验操作中重要的疏漏是没有平衡摩擦力或者摩擦力平衡不足.
 如图,质量为4kg的物体静止在水平面上.现用大小为40N,与水平方向夹角为37°的斜向上的力拉物体,使物体沿水平面做匀加速运动.(g取10m/s2,sin37°=0.6,cos37°=0.8)
如图,质量为4kg的物体静止在水平面上.现用大小为40N,与水平方向夹角为37°的斜向上的力拉物体,使物体沿水平面做匀加速运动.(g取10m/s2,sin37°=0.6,cos37°=0.8)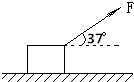 如图所示,质量为m=4kg的物体与水平地面间的动摩擦因数μ=0.3,现用与水平方向成θ=37°的力F拉物体,使物体在水平地面上匀速运动,求:
如图所示,质量为m=4kg的物体与水平地面间的动摩擦因数μ=0.3,现用与水平方向成θ=37°的力F拉物体,使物体在水平地面上匀速运动,求: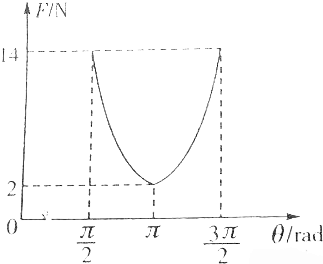 在“研究两个共点力合成“的实验中得到如图所示的合力F与两个分力的夹角的关系图.问:
在“研究两个共点力合成“的实验中得到如图所示的合力F与两个分力的夹角的关系图.问: