��Ŀ����
 ��2010?Խ������ģ����ͼ��ʾ������ԴS���Բ��ϲ�������Ϊm�������Ϊ+q�����ӣ��������ƣ������Ӵ�O1��Ʈ��һ��ˮƽ����ļ��ٵ糡�����ٲ��ƣ����پ���С��O2�������������ǿ�糡����ǿ�ų����糡ǿ�ȴ�СΪE���Ÿ�Ӧǿ�ȴ�СΪB1��������ͼ������PQ��MN֮�������ˮƽ���ҵ���ǿ�ų����ų���Χ�㹻�Ÿ�Ӧǿ�ȴ�СΪB2��һ���۳�ֱ�ǵ�Ӳ������Ƭabc�������磬���Ⱥͺ�ȶ���С�ɺ��ԣ�������PQ��MN֮�䣬����ͼ��ͼ��a��c����ֱ�λ��PQ��MN�ϣ�ab=bc=L��a=45�㣮��������ͼ������O2O3���ӳ��߽���PQ��MN֮�������
��2010?Խ������ģ����ͼ��ʾ������ԴS���Բ��ϲ�������Ϊm�������Ϊ+q�����ӣ��������ƣ������Ӵ�O1��Ʈ��һ��ˮƽ����ļ��ٵ糡�����ٲ��ƣ����پ���С��O2�������������ǿ�糡����ǿ�ų����糡ǿ�ȴ�СΪE���Ÿ�Ӧǿ�ȴ�СΪB1��������ͼ������PQ��MN֮�������ˮƽ���ҵ���ǿ�ų����ų���Χ�㹻�Ÿ�Ӧǿ�ȴ�СΪB2��һ���۳�ֱ�ǵ�Ӳ������Ƭabc�������磬���Ⱥͺ�ȶ���С�ɺ��ԣ�������PQ��MN֮�䣬����ͼ��ͼ��a��c����ֱ�λ��PQ��MN�ϣ�ab=bc=L��a=45�㣮��������ͼ������O2O3���ӳ��߽���PQ��MN֮���������1������ٵ�ѹU1��
��2������������Ӳ������Ƭ�������ٶȴ�С���䣬������ѭ��ķ��䶨�ɣ���ô����������Ƭ��һ�������ڶ�������ǰ��ʲô�˶���
��3��������PQ��MN֮����������˶�����ʱ��t����·��s��
��������1�����Ӿ������ϳ�ʱ���糡�����£������������ϣ������ٶȴ�ֱ���ʺ���Ϊ�㣬����ƽ��������ʽ����ٶȣ�
��2��������ų���һ����ײ���ٶ����ϣ����������ṩ������������ac�ߴ�ֱ��ƽ����������Բ���˶�������һȦ����ab���ڲ���ײ����ײ��ˮƽ�����˶�����bc�߶�����ײ������ac�ߴ�ֱ��ƽ�������ٴ�����Բ���˶����־���һȦ����b�������ײ��ˮƽ�����뿪�ų���
��3���ȷ������˶��켣���ٷ�����ֱ���˶�������Բ���˶����ۣ���������Բ���˶����ȼ���뾶�����ڣ��ٸ��ݹ켣���㣮
��2��������ų���һ����ײ���ٶ����ϣ����������ṩ������������ac�ߴ�ֱ��ƽ����������Բ���˶�������һȦ����ab���ڲ���ײ����ײ��ˮƽ�����˶�����bc�߶�����ײ������ac�ߴ�ֱ��ƽ�������ٴ�����Բ���˶����־���һȦ����b�������ײ��ˮƽ�����뿪�ų���
��3���ȷ������˶��켣���ٷ�����ֱ���˶�������Բ���˶����ۣ���������Բ���˶����ȼ���뾶�����ڣ��ٸ��ݹ켣���㣮
����⣺��1�����������������������˶���Eq=qv0B1��
��v0=
�ɶ��ܶ����� qU1=
�� U1=
�����ٵ�ѹΪ
��
��2����������ab���Դ�СΪv0���ٶȴ�ֱ�ų������˶������������������ڴ�ֱ�ڴų���ƽ����������Բ���˶���ת��һ�ܺ�ﵽab���²���
��3����qv0B2=m
�� R=
=
��T=
�� T=
�����ڴų��й�����2�Σ���Բ���˶���ʱ��Ϊ t1=2T=
��Բ���˶���·��Ϊ s1=2?2��R=
��ˮƽ�������˶���·�� s2=
R��
������ʱ��Ϊt2=
=
��������PQ��MN֮����������˶�����ʱ��t=t1+t2=
+
��·��s=s1+s2=
+
L
��������PQ��MN֮����������˶�����ʱ��Ϊ
+
����·��Ϊ
+
L��
��v0=
| E |
| B1 |
�ɶ��ܶ����� qU1=
| 1 |
| 2 |
| mv | 2 0 |
�� U1=
| mE2 | ||
2q
|
�����ٵ�ѹΪ
| mE2 | ||
2q
|
��2����������ab���Դ�СΪv0���ٶȴ�ֱ�ų������˶������������������ڴ�ֱ�ڴų���ƽ����������Բ���˶���ת��һ�ܺ�ﵽab���²���
��3����qv0B2=m
| ||
| R |
�� R=
| mv0 |
| qB2 |
| mE |
| qB1B2 |
��T=
| 2��R |
| v0 |
�� T=
| 2��m |
| qB2 |
�����ڴų��й�����2�Σ���Բ���˶���ʱ��Ϊ t1=2T=
| 4��m |
| qB2 |
��Բ���˶���·��Ϊ s1=2?2��R=
| 4��mE |
| qB1B2 |
��ˮƽ�������˶���·�� s2=
| 2 |
������ʱ��Ϊt2=
| S |
| v0 |
| ||
| E |
��������PQ��MN֮����������˶�����ʱ��t=t1+t2=
| 4��m |
| qB2 |
| ||
| E |
��·��s=s1+s2=
| 4��mE |
| qB1B2 |
| 2 |
��������PQ��MN֮����������˶�����ʱ��Ϊ
| 4��m |
| qB2 |
| ||
| E |
| 4��mE |
| qB1B2 |
| 2 |
�����������еĸ��ϳ������ٶ�ѡ��Ĺ��ܣ�����ų�������ݶ���ѧ������ȷ���˶��켣���ٽ��м��㣮

��ϰ��ϵ�д�
�����Ŀ
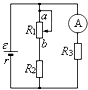 ��2010?Խ������ģ����ͼ��ʾ��һʵ���·ͼ���ڻ�����ͷ��a�˻���b�˵Ĺ����У����б�����ȷ���ǣ�������
��2010?Խ������ģ����ͼ��ʾ��һʵ���·ͼ���ڻ�����ͷ��a�˻���b�˵Ĺ����У����б�����ȷ���ǣ������� ��2010?Խ������ģ����ͼ��ʾ�������Ĵ��ʹ���ˮƽ��ļнǦ�=30�㣬Ƥ���ڵ綯���Ĵ����£�ʼ�ձ���v0=2m/s���������У��ְ�һ����m=10kg�Ĺ������ɿ����ʵ㣩�������Ƥ���ĵˣ���ʱ��t=1.9s�����������͵�h=1.5m�ĸߴ���ȡg=10m/s2����
��2010?Խ������ģ����ͼ��ʾ�������Ĵ��ʹ���ˮƽ��ļнǦ�=30�㣬Ƥ���ڵ綯���Ĵ����£�ʼ�ձ���v0=2m/s���������У��ְ�һ����m=10kg�Ĺ������ɿ����ʵ㣩�������Ƥ���ĵˣ���ʱ��t=1.9s�����������͵�h=1.5m�ĸߴ���ȡg=10m/s2����