题目内容
11.某同学用气垫导轨做侧滑块加速度和验证机械能守恒定律实验,A、B为气垫导轨上的两个光电门,当滑块在气垫导轨上滑动通过两光电门时,连接在光电门上的数字计时器记录滑块上的挡光片挡光时间,两光电门间的距离为L.
(1)先用一螺旋测微器测量挡光片的宽度,如图2所示,读数为d=0.6725cm.
(2)实验开始先调节气垫导轨下面的螺钉,使气垫导轨水平,在不增加其他仪器的情况下,如何判定气垫导轨是否水平?
取下牵引重物,M放在任意位置不动,或取下牵相重物,轻推滑块,数字计时器记录每一个光电门的电束被挡住的时间都相等
(3)让滑块在图示1位置由静止开始在悬挂重物的牵引下向左运动,牵引滑块的细绳始终保持水平,滑块通过A、B两光电门的时间分别为t1、t2,则此次运动过程中,滑块运动的加速度大小为$\frac{{d}^{2}}{2L}$($\frac{1}{{t}_{1}^{2}}$-$\frac{1}{{t}_{2}^{2}}$)(用题设中各物理量符号表示).要利用此过程验证机械能守恒定律,还需要测量的物理量为滑块的质量M,以及悬挂重物的质量m,(填物理量及符号),要验证机械能守恒的表达式为mgL=$\frac{1}{2}$(M+m)d2(($\frac{1}{{t}_{1}^{2}}$-$\frac{1}{{t}_{2}^{2}}$)(用顺设中各物理量符号表示).
分析 (1)根据螺旋测微器的读数方法可明确对应的读数,注意在读可动部分时需要估读;
(2)导轨水平时,滑块在不受外力的情况下应处于平衡状态;故小车可以做匀速直线运动或静止;
(3)根据平均速度公式可求得经过光电门的速度,再由速度和位移公式可求得加速度;根据机械能守恒定律可明确对应的表达式.
解答 解:(1)螺旋测微器的读数为:
d=6.5+22.5×0.01mm=6.725mm=0.6725cm
(2)气垫导轨处于水平时,滑块受力平衡,故可以取下牵引重物,M放在任意位置不动,或取下牵相重物,轻推滑块,数字计时器记录每一个光电门的电束被挡住的时间都相等;
(3)经过光电门的速度v=$\frac{d}{t}$;
由v2-v02=2ax可知,
($\frac{d}{{t}_{1}}$)2-($\frac{d}{{t}_{2}}$)2=2aL;
解得:
a=$\frac{{d}^{2}}{2L}$($\frac{1}{{t}_{1}^{2}}$-$\frac{1}{{t}_{2}^{2}}$)
要想验证机械能守恒,还需要测量滑块的质量M,以及悬挂重物的质量m,根据机械能守恒定律可知:
mgL=$\frac{1}{2}$(M+m)d2(($\frac{1}{{t}_{1}^{2}}$-$\frac{1}{{t}_{2}^{2}}$);
故答案为:(1)0.6725;(2)可以取下牵引重物,M放在任意位置不动,或取下牵相重物,轻推滑块,数字计时器记录每一个光电门的电束被挡住的时间都相等;
(3)滑块的质量M,以及悬挂重物的质量m;
mgL=$\frac{1}{2}$(M+m)d2(($\frac{1}{{t}_{1}^{2}}$-$\frac{1}{{t}_{2}^{2}}$);
点评 掌握螺旋测微器读数的方法:固定刻度读数+可动刻度读数,知道在极短时间内的平均速度可以表示瞬时速度和匀变速直线运动的速度位移公式应用.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案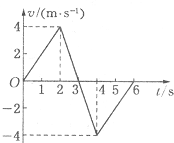
| A. | 第2 s内和第3 s内速度方向相反 | |
| B. | 第2 s内和第3 s内的加速度方向相反 | |
| C. | 第3 s内速度方向与加速度方向相反 | |
| D. | 第3末物体的位移最大 |
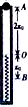 如图所示,在一直立的光滑管内放置一轻质弹簧,上端O点与管口A的距离为2x0,一质量为m的小球从管口由静止下落,将弹簧压缩至最低点B,压缩量为x0,不计空气阻力,则( )
如图所示,在一直立的光滑管内放置一轻质弹簧,上端O点与管口A的距离为2x0,一质量为m的小球从管口由静止下落,将弹簧压缩至最低点B,压缩量为x0,不计空气阻力,则( )| A. | 小球运动的最大速度等于2$\sqrt{g{x}_{0}}$ | B. | O到B过程加速度一直增大 | ||
| C. | O到B过程速度先增大后减小 | D. | 弹簧的最大弹性势能为3mgx0 |
 如图,用一平行于斜面的力F推滑块,使滑块静止于粗糙的斜面上,现增大力F,滑块和斜面体始终静止,则( )
如图,用一平行于斜面的力F推滑块,使滑块静止于粗糙的斜面上,现增大力F,滑块和斜面体始终静止,则( )| A. | 斜面对滑块的摩擦力一定增大 | B. | 斜面对滑块的摩擦力可能不变 | ||
| C. | 地面对斜面体的摩擦力增大 | D. | 地面对斜面体的支持力增大 |
| A. | 无卢瑟福依据α粒子散射实验的现象提出了原子的“核式结构”理论 | |
| B. | ${\;}_{1}^{1}$H+${\;}_{1}^{2}$H→${\;}_{2}^{2}$He+y是核聚变反应方程 | |
| C. | β射线是由原子核外的电子电离产生 | |
| D. | α射线是由氢原子核衰变产生 | |
| E. | 通过化学反应不能改变放射性物质的半衰期 |
 如图所示,A线圈接一灵敏电流计G,B线框放在匀强磁场中,B线框的电阻不计,具有一定电阻的导体棒可沿线框无摩擦滑动,今用恒力F向右拉CD由静止开始运动,B线框足够长,则CD杆运动情况和通过电流表G中的电流变化情况是( )
如图所示,A线圈接一灵敏电流计G,B线框放在匀强磁场中,B线框的电阻不计,具有一定电阻的导体棒可沿线框无摩擦滑动,今用恒力F向右拉CD由静止开始运动,B线框足够长,则CD杆运动情况和通过电流表G中的电流变化情况是( )| A. | CD杆一直做匀速运动 | |
| B. | CD杆先做加速运动,再做减速运动,最后停止 | |
| C. | G中电流向上,强度逐渐增强 | |
| D. | G中电流向下,强度逐渐减弱,最后为零 |
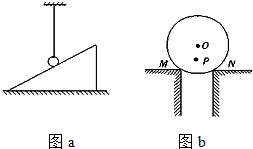 如图a中,小球用细线悬于天花板上,同时小球还与光滑斜面接触;图b中,光滑小球静止在两桌子之间,点O和点p分别是球的圆心和重心,请画出两图中小球所受的弹力示意图.
如图a中,小球用细线悬于天花板上,同时小球还与光滑斜面接触;图b中,光滑小球静止在两桌子之间,点O和点p分别是球的圆心和重心,请画出两图中小球所受的弹力示意图.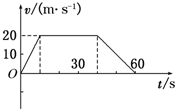 汽车由静止开始在平直的公路上行驶,0~60s内汽车的速度随时间变化的图线如图所示.
汽车由静止开始在平直的公路上行驶,0~60s内汽车的速度随时间变化的图线如图所示.