题目内容
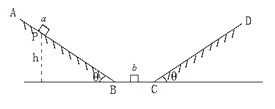
【题目】如图所示,有两足够长倾角皆为![]() 的粗糙斜面AB和CD通过一小段平滑的园弧与光滑的水平面BC连接,两质量相等的可视为质点的小滑块
的粗糙斜面AB和CD通过一小段平滑的园弧与光滑的水平面BC连接,两质量相等的可视为质点的小滑块![]() 和
和![]() 与斜面AB,CD的动摩擦因数因数分别为
与斜面AB,CD的动摩擦因数因数分别为![]() ,
,![]() 。开始时小滑块
。开始时小滑块![]() 在斜面AB上距水平面高为
在斜面AB上距水平面高为![]() 处的P点由静止下滑,物块
处的P点由静止下滑,物块![]() 静止在水平面BC上。已知小滑块
静止在水平面BC上。已知小滑块![]() 与
与![]() 的碰撞为弹性碰撞,重力加速度
的碰撞为弹性碰撞,重力加速度![]() ,sin37°=0.6,cos=37°=0.8。求:
,sin37°=0.6,cos=37°=0.8。求:
(1)小滑块![]() 第一次与小滑块
第一次与小滑块![]() 碰撞前的速度
碰撞前的速度![]() ;
;
(2)小滑块![]() 第一次碰撞后,沿CD斜面上滑的距离
第一次碰撞后,沿CD斜面上滑的距离![]() ;
;
(3)小滑块![]() 、
、![]() 在斜面上运动的总路程
在斜面上运动的总路程![]() 与
与![]() 。
。
【答案】(1)![]() (2)0.5m(3)
(2)0.5m(3)![]() ,
, ![]()
【解析】
(1)小滑块a第一次与小滑块b碰撞前,由动能定理:![]()
解得:![]()
(2)因ab质量相等,则ab发生弹性碰撞时满足动量守恒和能量守恒:
![]()
![]()
解得![]() ,
,![]()
物块b滑上最高点的过程中由动能定理:![]()
解得s1=0.5m
(3)b滑到斜面底端时的速度:![]()
解得![]()
b与a碰后再次交换速度,则此时b的速度为零,a的速度为v4=2m/s,则a沿斜面上升速度减为零时:![]()
解得:s2=0.2m
返回到底端时:![]() ,
,
解得![]()
在底部a与b碰撞后再次交换速度,则b的速度:![]() ,
,
上升到顶端时:![]() ;
;
解得s3=0.05m;
因每次滑块上升到顶端再回到底端时的路程成等比关系,其中公比q=0.1, 由数学知识可知:![]() ;(
;(![]() )
)
![]()

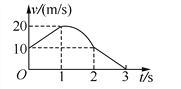
【题目】小华和小明在“描绘小灯泡伏安特性曲线”的实验中,将实验数据记录在下表中:
电压U/V | 0.00 | 0.20 | 0.40 | 0.70 | 1.00 | 1.30 | 1.70 | 2.10 | 2.50 |
电流I/A | 0.00 | 0.14 | 0.24 | 0.26 | 0.37 | 0.40 | 0.43 | 0.45 | 0.46 |
(1)实验室有两种滑动变阻器供选择:
A.滑动变阻器(阻值范围0~10 Ω、额定电流3 A)
B.滑动变阻器(阻值范围0~2 000 Ω、额定电流1 A)
实验中选择的滑动变阻器是________.(填写字母序号)
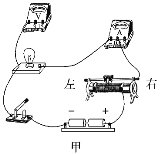
(2)在图甲中用笔画线代替导线,将实验电路连接完整.________
(3)开关闭合前,滑动变阻器的滑片应滑至________(选填“左”或“右”)端.