题目内容
9. 如图所示,光滑杆AB长为L,B端固定一根劲度系数为k、原长为x0的轻弹簧,质量为m的小球套在光滑杆上并与弹簧的上端连接.OO′为过B点的竖直轴,杆与水平面间的夹角始终为θ,重力加速度为g.
如图所示,光滑杆AB长为L,B端固定一根劲度系数为k、原长为x0的轻弹簧,质量为m的小球套在光滑杆上并与弹簧的上端连接.OO′为过B点的竖直轴,杆与水平面间的夹角始终为θ,重力加速度为g.(1)当小球随杆一起绕OO′轴匀速转动时,弹簧伸长量为△x1,求小球随杆匀速转动的角速度ω;
(2)杆保持静止状态,让小球从弹簧的原长位置由静止释放,已知弹簧形变时弹簧内的弹性势能EP=$\frac{1}{2}$kx2,x为弹簧形变量,求小球下滑过程中的最大速度;
(3)若θ=300,撤去弹簧,当杆绕OO′轴以角速度ω0=$\sqrt{\frac{g}{L}}$匀速转动时,小球恰好在杆上某一位置随杆在水平面内匀速转动,小球受轻微扰动后将沿杆向上滑动,到达A端时小球沿杆方向的速度大小为v0,求小球从开始滑动到离开杆过程中,杆对球所做的功W.
分析 (1)对小球分析,抓住竖直方向上的合力为零,水平方向上的合力提供向心力,列式联立求出匀速转动的角速度.
(2)当小球的加速度为零时,速度最大,根据牛顿第二定律结合动能定理列式求解.
(3)根据牛顿第二定律求出小球做匀速转动时距离B点的距离,求出此时小球的动能,结合最高点的动能,运用动能定理求出杆对小球做功的大小.
解答 解:(1)对小球受力分析,在水平方向上有:${F_{N1}}sinθ+k•△{x_1}cosθ=m({x_0}+△{x_1})cosθ•{ω^2}$
竖直方向上有:FN1cosθ=mg+k△x1sinθ
解得:$ω=\sqrt{\frac{{mgsinθ+k△{x_1}}}{{m({x_0}+△{x_1}){{cos}^2}θ}}}$=$\frac{1}{cosθ}\sqrt{\frac{{mgsinθ+k△{x_1}}}{{m({x_0}+△{x_1})}}}$
(2)小球下滑过程中,当加速度等于零时速度最大,设弹簧被压缩了△x2时小球速度最大,
有mgsinθ=k△x2
根据动能定理得:$mg△{x_2}•sinθ=\frac{1}{2}mv_m^2+\frac{1}{2}k△x_2^2$
解得:${v_m}=gsinθ\sqrt{\frac{m}{k}}$
(3)小球恰好在杆上某一位置随杆在水平面内匀速转动时,设小球距B端距离为L0,
有FN2cos30°=mg
${F}_{N2}sin30°=m{l}_{0}cos30°•{{ω}_{0}}^{2}$
小球从开始滑动到离开杆过程中,根据动能定理有
$W-mg(L-{L}_{0})sin30°=\frac{1}{2}m[{v}_{0}^{2}+{(Lcos30°•{ω}_{0})}^{2}]-$$\frac{1}{2}m{({L}_{0}cos30°•{ω}_{0})}^{2}$
解得:$W=\frac{1}{2}mv_0^2+\frac{3}{8}mgL$
答:(1)小球随杆匀速转动的角速度ω为$\frac{1}{cosθ}\sqrt{\frac{mgsinθ+k△{x}_{1}}{m({x}_{0}+△{x}_{1})}}$;
(2)小球下滑过程中的最大速度为$gsinθ\sqrt{\frac{m}{k}}$;
(3)小球从开始滑动到离开杆过程中,杆对球所做的功W为$\frac{1}{2}m{v}_{0}^{2}+\frac{3}{8}mgL$.
点评 本题考查了动能定理、牛顿第二定律、胡克定律与圆周运动的综合,知道小球做匀速转动时,靠径向的合力提供向心力,由静止释放时,加速度为零时速度最大.

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案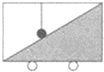 如图所示,水平向左运动的小车内有一固定光滑斜面,一个小球通过细绳与车顶相连,细绳始终保持竖直,关于小球的受力情况,下列说法正确的是( )
如图所示,水平向左运动的小车内有一固定光滑斜面,一个小球通过细绳与车顶相连,细绳始终保持竖直,关于小球的受力情况,下列说法正确的是( )| A. | 小球可能只受重力和支持力 | |
| B. | 小球可能只受重力和拉力 | |
| C. | 斜面对小球的作用力不可能小于小球的重力 | |
| D. | 小球不可能受到三个力的作用 |
| A. | 电场强度处处相同的区域内,电势也一定处处相同 | |
| B. | 电场强度处处为零的区域内,电势也一定处处为零 | |
| C. | 电场强度的方向不一定跟等势面垂直的 | |
| D. | 沿着电场强度的方向,电势一定是不断降低的 |
| A. | 物体只要受到变力的作用,就会做曲线运动 | |
| B. | 物体在方向不变的外力作用下一定会做直线运动 | |
| C. | 物体在方向不断变化的外力作用下一定会做曲线运动 | |
| D. | 物体在大小不变的外力作用下必做匀变速曲线运动 |
 如图所示,a、b两物块质量分别为m、3m,用不计质量的细绳相连接,悬挂在定滑轮的两侧.开始时,a、b两物块距离地面高度相同,用手托住物块b,然后由静止释放,直至a、b物块间高度差为h,不计滑轮质量和一切摩擦,重力加速度为g.在此过程中,下列说法正确的是( )
如图所示,a、b两物块质量分别为m、3m,用不计质量的细绳相连接,悬挂在定滑轮的两侧.开始时,a、b两物块距离地面高度相同,用手托住物块b,然后由静止释放,直至a、b物块间高度差为h,不计滑轮质量和一切摩擦,重力加速度为g.在此过程中,下列说法正确的是( )| A. | 物块a的机械能守恒 | |
| B. | 物块b的机械能减少了$\frac{2}{3}$mgh | |
| C. | 物块b机械能的减少量等于物块a机械能的增加量 | |
| D. | 物块a、b与地球组成的系统机械能守恒 |
 一质量为2kg的质点在xOy平面内运动,在x方向的s-t图象和y方向的v-t图象分别如图所示.则该质点( )
一质量为2kg的质点在xOy平面内运动,在x方向的s-t图象和y方向的v-t图象分别如图所示.则该质点( )| A. | 初速度大小为5m/s | B. | 所受的合外力为3N | ||
| C. | 做匀变速曲线运动 | D. | 初速度方向与合外力方向垂直 |
 如图所示,足够大的匀强磁场其方向竖直向下,磁场中有光滑的足够大的水平桌面,在桌面上平放着内壁光滑,底部有带电小球的试管,试管在水平拉力F作用下向右匀速运动,带电小球能从管口处飞出.关于带电小球及其在离开试管前、后的运动,下列说法中不正确的是( )
如图所示,足够大的匀强磁场其方向竖直向下,磁场中有光滑的足够大的水平桌面,在桌面上平放着内壁光滑,底部有带电小球的试管,试管在水平拉力F作用下向右匀速运动,带电小球能从管口处飞出.关于带电小球及其在离开试管前、后的运动,下列说法中不正确的是( )| A. | 小球带正电 | |
| B. | 离开试管前洛伦兹力对小球做正功,离开试管后洛伦兹力对小球不做功 | |
| C. | 离开试管前小球运动的轨迹是一条抛物线 | |
| D. | 离开试管后沿着磁感线方向可以看到小球做逆时针方向的圆周运动 |

