题目内容
 (2011?厦门模拟)如图所示,一面积为S单匝圆形金属线圈与阻值为R的电阻连结成闭合回路,不计圆形金属线圈及导线的电阻.线圈内存在一个方向垂直纸面向内、磁感应强度均匀增加且变化率为k的磁场Bt.电阻两端并联一对平行金属板M、N,N板右侧xOy坐标系(坐标原点O在N板的下端)的第一象限内,有垂直纸面向外的匀强磁场,磁场边界OA和y轴的夹角∠AOy=45°,AOx区域为无场区.在靠近M板处的P点由静止释放一质量为m,带电量为+q的粒子(不计重力),经过N板的小孔,从Q(0,a)点垂直y轴进入第I象限,经OA上某点离开磁场,最后垂直x轴离开第I象限.求:
(2011?厦门模拟)如图所示,一面积为S单匝圆形金属线圈与阻值为R的电阻连结成闭合回路,不计圆形金属线圈及导线的电阻.线圈内存在一个方向垂直纸面向内、磁感应强度均匀增加且变化率为k的磁场Bt.电阻两端并联一对平行金属板M、N,N板右侧xOy坐标系(坐标原点O在N板的下端)的第一象限内,有垂直纸面向外的匀强磁场,磁场边界OA和y轴的夹角∠AOy=45°,AOx区域为无场区.在靠近M板处的P点由静止释放一质量为m,带电量为+q的粒子(不计重力),经过N板的小孔,从Q(0,a)点垂直y轴进入第I象限,经OA上某点离开磁场,最后垂直x轴离开第I象限.求:(1)平行金属MN获得的电压U;
(2)yOA区域匀强磁场的磁感应强度B;
(3)若改变磁感应强度的大小,带电粒子进入磁场偏转后能打到N板的右侧,设粒子与N板碰撞前后电量保持不变并以相同的速率反弹,不计粒子与N板碰撞的作用时间,则带电粒子在磁场中运动的极限时间是多少?
分析:(1)根据法拉第电磁感应定律,求出闭合电路的电动势即平行金属MN获得的电压U;
(2)正确画出粒子运动的轨迹图,根据几何关系找出粒子运动 的半径的大小,代人公式求得磁场的磁感应强度;
(3)当r′为无穷小,经过n个半圆运动,最后一次打到O点.
(2)正确画出粒子运动的轨迹图,根据几何关系找出粒子运动 的半径的大小,代人公式求得磁场的磁感应强度;
(3)当r′为无穷小,经过n个半圆运动,最后一次打到O点.
解答:解:(1)根据法拉第电磁感应定律,闭合电路的电动势为:E=
=
?S=kS①
因MN与电阻并联,故MN获得的电压:U=UR=E=kS②
(2)带电粒子在MN间做匀加速直线运动,有:qU=
mv 2③
带电粒子进入磁场区域运动轨迹如图所示,
有:qvB=m
④
由几何关系得:r+rtan45°=a⑤
由②③④⑤得:B=
⑦
(3)设粒子运动圆周半径为r′,r′=
,当r′越小,最后一次打到N板的点的越靠近O点,在磁场中圆周运动累积路越大,时间越长,当r′为无穷小,经过n个半圆运动,最后一次打到O点,有:n=
⑧
圆周运动周期:T=
⑨
最长的根限时间:tm=n
⑨
由②③⑧⑨⑩式得:tm=
=
⑩
答:(1)平行金属MN获得的电压kS;(2)yOA区域匀强磁场的磁感应强度B=
;(3)带电粒子在磁场中运动的极限时间是
.
| △φ |
| △t |
| △B |
| △t |
因MN与电阻并联,故MN获得的电压:U=UR=E=kS②
(2)带电粒子在MN间做匀加速直线运动,有:qU=
| 1 |
| 2 |
带电粒子进入磁场区域运动轨迹如图所示,

有:qvB=m
| v 2 |
| r |
由几何关系得:r+rtan45°=a⑤
由②③④⑤得:B=
| 2 |
| a |
|
(3)设粒子运动圆周半径为r′,r′=
| mv |
| qB |
| a |
| 2r′ |
圆周运动周期:T=
| 2π?r′ |
| v |
最长的根限时间:tm=n
| T |
| 2 |
由②③⑧⑨⑩式得:tm=
| π?a |
| 2v |
| π?a |
| 2 |
|
答:(1)平行金属MN获得的电压kS;(2)yOA区域匀强磁场的磁感应强度B=
| 2 |
| a |
|
| π?a |
| 2 |
|
点评:本题是粒子在磁场中匀速圆周运动和电磁感应的综合.磁场中圆周运动常用方法是画轨迹,由几何知识求半径.

练习册系列答案
相关题目
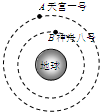 (2011?厦门模拟)据中新社3月10日消息,我国将于2011年上半年发射“天宫一号”目标飞行器,2011年下半年发射“神舟八号”飞船并与“天宫一号”实现对接.某同学得知上述消息后,画出“神舟八号”和“天宫一号”绕地球做匀速圆周运动的假想图如图所示,A代表“天宫一号”,B代表“神舟八号”,虚线为各自的轨道.由此假想图,可以判断( )
(2011?厦门模拟)据中新社3月10日消息,我国将于2011年上半年发射“天宫一号”目标飞行器,2011年下半年发射“神舟八号”飞船并与“天宫一号”实现对接.某同学得知上述消息后,画出“神舟八号”和“天宫一号”绕地球做匀速圆周运动的假想图如图所示,A代表“天宫一号”,B代表“神舟八号”,虚线为各自的轨道.由此假想图,可以判断( )