题目内容
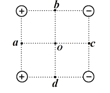
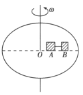
【题目】如图所示,在匀速转动的圆盘上,沿半径方向放置以细线相连的质量均为![]() 的A、B两个小物块(细线伸直)。A离轴心r1=10cm,B离轴心r2=20cm,A、B两与圆盘面间相互作用的最大静摩擦力为其重力的0.3倍,取g=10m/s2。求:
的A、B两个小物块(细线伸直)。A离轴心r1=10cm,B离轴心r2=20cm,A、B两与圆盘面间相互作用的最大静摩擦力为其重力的0.3倍,取g=10m/s2。求:
(1)若细线上刚要出现张力时,圆盘的角速度![]() ;
;
(2)欲使A、B与圆盘面间不发生相对滑动,则圆盘转动的最大角速度![]() ;
;
(3)当圆盘转速达到A、B刚好不滑动时,烧断细线,则A、B将怎样运动?
【答案】(1)![]() ;(2)
;(2)![]() ;(3)A随盘一起转动,B将做离心运动
;(3)A随盘一起转动,B将做离心运动
【解析】
(1)当![]() 所需受到的摩擦力达到最大静摩擦力时,细线就要出现张力,对B有
所需受到的摩擦力达到最大静摩擦力时,细线就要出现张力,对B有
![]()
解得![]()
(2)当所受静摩擦力増大到最大静摩擦力时,圆盘的角速度达到最大值![]() ,超过
,超过![]() 时,
时,![]() 、
、![]() 将相对圆盘滑动,设细线中的张力为
将相对圆盘滑动,设细线中的张力为![]() ,对
,对![]()
![]()
对![]()
![]()
解得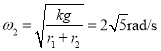
(3)烧断细线时,![]() 做圆周运动所需向心力
做圆周运动所需向心力
![]()
又因为最大静摩擦力为![]() ,所以
,所以![]() 随盘一起转动。
随盘一起转动。![]() 此时所需向心力
此时所需向心力
![]()
大于它的最大静摩擦力![]() ,因此
,因此![]() 将做离心运动。
将做离心运动。

练习册系列答案
相关题目