题目内容
5.一个初速度为零的质子,经过电压为U的电场加速后,垂直进入磁感应强度为B的匀强磁场,已知质子质量为m,电量为q,求:①质子进入磁场中的速度大小;
②质子在磁场中运动的轨道半径.
分析 由动能定理即可求出粒子进入磁场时的速度,由洛伦兹力提供向心力即可求得粒子的半径.
解答 解:①粒子在电场中加速.由动能定理得:$qU=\frac{1}{2}m{v}^{2}$
得:$v=\sqrt{\frac{2qU}{m}}$
②带电粒子在磁场中受到的洛伦兹力:$f=qvB=qB•\sqrt{\frac{2qU}{m}}$
由洛伦兹力提供向心力得:$qvB=\frac{m{v}^{2}}{r}$
所以:$r=\frac{mv}{qB}=\frac{1}{B}•\sqrt{\frac{2mU}{q}}$
答:①质子进入磁场中的速度大小$\sqrt{\frac{2qU}{m}}$;
②质子在磁场中运动的轨道半径$\frac{1}{B}•\sqrt{\frac{2mU}{q}}$.
点评 考查粒子在电场中加速与磁场中偏转,掌握动能定理与牛顿第二定律的应用,注意运动半径与已知长度的关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.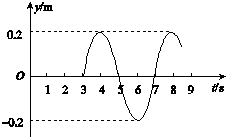 一列简谐横波沿直线传播,以波源O由平衡位置开始振动为计时零点,质点A的振动图象如图所示,已知O、A的平衡位置相距1.2m.以下判断正确的是( )
一列简谐横波沿直线传播,以波源O由平衡位置开始振动为计时零点,质点A的振动图象如图所示,已知O、A的平衡位置相距1.2m.以下判断正确的是( )
 一列简谐横波沿直线传播,以波源O由平衡位置开始振动为计时零点,质点A的振动图象如图所示,已知O、A的平衡位置相距1.2m.以下判断正确的是( )
一列简谐横波沿直线传播,以波源O由平衡位置开始振动为计时零点,质点A的振动图象如图所示,已知O、A的平衡位置相距1.2m.以下判断正确的是( )| A. | 波长为1.2 m | |
| B. | 波源起振方向沿y轴正方向 | |
| C. | 波速大小为0.4m/s | |
| D. | 质点A的加速度在t=4 s时最大 | |
| E. | 质点A在t=3.5s至t=4.5s的运动的路程为0.2m |
13.下列物体运动过程中,机械能守恒的是( )
| A. | 降落伞匀速下落 | B. | 汽车制动后在公路上滑行 | ||
| C. | 升降机加速上升 | D. | 小球做自由落体运动 |
20.一通电直导线用细线悬挂于匀强磁场中,磁场及电流方向如图所示.通电导线所受安培力的方向是( )
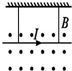

| A. | 竖直向下 | B. | 水平向右 | C. | 竖直向上 | D. | 水平向左 |
10.水平地面上的物体重力为10N,外力F竖直向上作用于该物体,F的大小为3N,则地面对该物体支持力的大小是( )
| A. | 0N | B. | 3N | C. | 7N | D. | 10N |
15.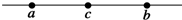 如图所示,a、b、c为电场中同一条电场线上的三点,其中c为ab的中点.已知a、b两点的电势分别为φa=3V,φb=9V,则下列叙述正确的是( )
如图所示,a、b、c为电场中同一条电场线上的三点,其中c为ab的中点.已知a、b两点的电势分别为φa=3V,φb=9V,则下列叙述正确的是( )
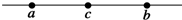 如图所示,a、b、c为电场中同一条电场线上的三点,其中c为ab的中点.已知a、b两点的电势分别为φa=3V,φb=9V,则下列叙述正确的是( )
如图所示,a、b、c为电场中同一条电场线上的三点,其中c为ab的中点.已知a、b两点的电势分别为φa=3V,φb=9V,则下列叙述正确的是( )| A. | c点的电势一定为6V | |
| B. | a点的场强Ea一定小于b点的场强Eb | |
| C. | 正电荷从a点运动到b点的过程中电势能一定增大 | |
| D. | 正电荷只受电场力作用从a点运动到b点的过程中动能一定增大 |
 在一个倾角为α的光滑斜面上,一物体一初速度v0冲上斜面,斜面足够长,g=10m/s2,求物体上升的最大高度?
在一个倾角为α的光滑斜面上,一物体一初速度v0冲上斜面,斜面足够长,g=10m/s2,求物体上升的最大高度?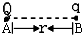 在真空中A点有一正电荷Q=2.0×10-4C,把检验电荷q=2.0×10-5C的负电荷置于B点,他们相距离r=2m,如图所示.求:
在真空中A点有一正电荷Q=2.0×10-4C,把检验电荷q=2.0×10-5C的负电荷置于B点,他们相距离r=2m,如图所示.求: